Pembahasan Soal Induksi Magnetik
Solusi Soal Induksi Magnetik
1. Soal
Kawat lingkaran $\frac{1}{4}$ dengan jari - jari 3 meter dialiri arus listrik 6 ampere. Besar induksi magnetik pada pusat lingkaran P adalah .... tesla (UMPTN 1996)
Kawat lingkaran $\frac{1}{4}$ dengan jari - jari 3 meter dialiri arus listrik 6 ampere. Besar induksi magnetik pada pusat lingkaran P adalah .... tesla (UMPTN 1996)
A. $\pi \times 10^{-5}$
B. $\pi \times 10^{-7}$
C. $4\pi \times 10^{-5}$
D. $4\pi \times 10^{-7}$
E. $7\pi \times 10^{-7}$
Pembahasan
Diketahui
$N=\frac{1}{4}$
$a = 3\; m$
$I = 6\; A$
Medan magnet di pusat
\begin{aligned}B_{p}&=\frac{\mu_{o}I}{2a}N\\ B_{p}&=\frac{4\pi \times 10^{-7}(6)}{2(3)}\frac{1}{4}\\ B_{p}&=\pi \times 10^{-7}\;Tesla\end{aligned}
Jawaban B
2. Soal
Kumparan bentuk segi empat dengan panjang 12 cm dan lebar 10 cm terdiri atas 40 lilitan dan dilalui arus 2 A. Kumparan berada dalam medan magnet 0,25 T. Besar torsi yang dialami kumparan adalah (SPMB 2005)
A. 0,06 Nm
B. 0,10 Nm
C. 0,24 Nm
D. 0,36 Nm
E. 0,48 Nm
Pembahasan
Diketahui
$A =p\times l =12\times 10\; cm^{2}=120\; cm^{2}=120\times 10^{-4}\;m^{2}$
$A =p\times l =12\times 10\; cm^{2}=120\; cm^{2}=120\times 10^{-4}\;m^{2}$
Torsi (momen gaya)
$\tau =BANI$
$\tau = 0,25\times 120\times 10^{-4}\times 40\times 2$
$\tau = 0,24\; Nm$
$\tau = 0,24\; Nm$
Jawaban C
3. Soal
Kawat bujursangkar ABCD dengan panjang sisi $2\sqrt{2}\;cm$ dialiri arus listrik searah 10 A seperti pada gambar berikut. Besar induksi magnetik di pusat bujur sangkar tersebut adalah:
A. $\sqrt{2}\times 10^{-4}\;Tesla$
B. $2\times 10^{-4}\;Tesla$
C. $2\sqrt{2}\times 10^{-4}\;Tesla$
D. $4\times 10^{-4}\;Tesla$
E. $4\times \sqrt{2}\times 10^{-4}\;Tesla$
Pembahasan
Medan magnet pada kawat terbatas
$\displaystyle B=\frac{\mu_{o}I}{4\pi a}(cos\; \alpha_{1}+cos\; \alpha_{2})$
Pada pusat persegi
$B_{AB}=B_{BC}=B_{CD}=B_{DA}=B$
$\displaystyle B=\frac{4\pi \times 10^{-7}\times 10}{4\pi \times \sqrt{2}\times 10^{-2}}(cos\; 45^{\circ}+cos\; 45^{\circ})$
$B=1\times 10^{-4}\; Tesla$
Karena searah, maka
$B_{total}-4B=4\times 10^{-4}Tesla$
$B_{total}-4B=4\times 10^{-4}Tesla$
atau menggunakan cara cepat
$\displaystyle B=\frac{\mu_{o}I}{\pi a}\sqrt{2}$
Jawaban D
4. Soal
Suatu partikel bermuatan dilepaskan dari keadaan diam pada suau daerah yang dipengaruhi medan listrik dan medan magnet yang konstan. Ketika partikel tersebut ternyata membentuk lintasan lurus, maka.... (SPMB 2005)
A. besar medan magnet lebih kecil medan listrik
B. besar medan magnet lebih besar medan listrik
C. besar medan magnet sama dengan medan listrik
D. arah medan magnet paralel terhadap medan listrik
E. arah medan magnet tegak lurus terhadap medan listrik
Pembahasan
Agar partikel bergerak lurus atau membentuk lintasan lurus maka besar gaya lorentz sama dengan gaya elektrostatis denga arah berlawanan.
Misalkan muatan positif memasuki medan listrik dan medan magnet
arah gaya elektrostatis (Fc) searah dengan arah E karena muatan positif
arah gaya lorentz (FL) tegak lurus dengan arah B, maka arah B dan E tegak lurus
Jawaban E
5. Soal
Sebuah partikel bermassa q dan bermassa m bergerak dalam lintasan lingkaran dengan jari - jari r dalam medan magnet serbasama B. Jika arah gerak partikel tegak lurus terhadap arah medan magnet, hitunglah momentum partikel. (UM UGM 2016)
A. $qB^{2}r$
B. $qBr^{2}$
C. $qBr$
D. $qBIr$
E. $q^{2}BIr$
Pembahasan
Muatan bergerak dalam medan magnet membentuk lintasan lingkaran (v dan B tegak lurus), maka:
momentum partikel:
\begin{aligned}F_{L}&=F_{sp}\\ Bqv&=\frac{mv^{2}}{R}\\ R&=\frac{mv}{Bq}\\ R&=\frac{p}{Bq}\\ p&=BqR\end{aligned}
Jawaban C
6. Soal
Dua buah partikel bermassa dan bermuatan yang identik bergerak melingkar beraturan masing - masing pada dua buah siklotron dengan medan magnet masing - masing adalah $B_{1}$ dan $B_{2}$. Jari - jari lintasan partikel masing - masing adalah $R_{1}$ dan $R_{2}$. Perbandingan energi kinetik kedua partikel tersebut $E_{k1}/E_{k2}$ adalah? (UM UGM 2016)
A. $\displaystyle \frac{B_{1}R_{1}}{B_{2}R_{2}}$
B. $\displaystyle \frac{B_{1}R_{2}}{B_{2}R_{1}}$
C. $\displaystyle \frac{B_{1}^{2}R_{1}^{2}}{B_{2}^{2}R_{2}^{2}}$
D. $\displaystyle \frac{B_{1}^{2}R_{2}^{2}}{B_{2}^{2}R_{1}^{2}}$
E. $\displaystyle \frac{B_{1}R_{1}^{2}}{B_{2}R_{2}^{2}}$
B. $\displaystyle \frac{B_{1}R_{2}}{B_{2}R_{1}}$
C. $\displaystyle \frac{B_{1}^{2}R_{1}^{2}}{B_{2}^{2}R_{2}^{2}}$
D. $\displaystyle \frac{B_{1}^{2}R_{2}^{2}}{B_{2}^{2}R_{1}^{2}}$
E. $\displaystyle \frac{B_{1}R_{1}^{2}}{B_{2}R_{2}^{2}}$
Pembahasan
Diketahui
$m_{1}=m_{2}$
$q_{1}=q_{2}$
bergerak melingkar di dalam medan magnet
\begin{aligned}F_{L}&=F_{sp}\\ Bqv&=\frac{mv^{2}}{R}\\ v&=\frac{BqR}{m}\end{aligned}
Energi kinetik
\begin{aligned}E_{k}&=\frac{1}{2}mv^{2}\\ E_{k}&=\frac{1}{2}m\left(\frac{BqR}{m}\right)^{2}\\ E_{k}&=\frac{1}{2}\frac{B^{2}q^{2}R^{2}}{m}\end{aligned}
Diperoleh
$E_{k}\sim B^{2}$
$E_{k}\sim R^{2}$
maka:
$\displaystyle \frac{E_{k1}}{E_{k2}}=\frac{B_{1}^{2}R_{1}^{2}}{B_{2}^{2}R_{2}^{2}}$
Jawaban C
7. Soal
Partikel bermuatan q bergerak dengan laju tetap memasuki medan magnet dan medan listrik secara tegak lurus (medan listrik tegak lurus medan magnet). Apabila besar induksi magnet 0,2 T dan kuat medan listrik $6\times 10^{4}\;V/m$ maka laju gerak partikel (dalam m/s) adalah? (UMPTN 1997)
A. $2\times 10^{5}$
B. $3\times 10^{5}$
C. $1,2\times 10^{6}$
D. $2\times 10^{6}$
E. $3,2\times 10^{6}$
Pembahasan
Diketahui
$B = 0,2\; T$
$E =6\times 10^{4}\;V/m$
Agar muatan tetap bergerak lurus maka:
7. Soal
Partikel bermuatan q bergerak dengan laju tetap memasuki medan magnet dan medan listrik secara tegak lurus (medan listrik tegak lurus medan magnet). Apabila besar induksi magnet 0,2 T dan kuat medan listrik $6\times 10^{4}\;V/m$ maka laju gerak partikel (dalam m/s) adalah? (UMPTN 1997)
A. $2\times 10^{5}$
B. $3\times 10^{5}$
C. $1,2\times 10^{6}$
D. $2\times 10^{6}$
E. $3,2\times 10^{6}$
Pembahasan
Diketahui
$B = 0,2\; T$
$E =6\times 10^{4}\;V/m$
Agar muatan tetap bergerak lurus maka:
\begin{aligned}F_{c}&=F_{L}\\ qE&=Bqv\\ v&=\frac{E}{B}\\ v&=\frac{6\times 10^{4}}{0,2}\\ v&=3\times 10^{5}\;m/s\end{aligned}
8. Soal
Jari - jari lintasan gerak proton di dalam sebuah sikotron proton adalah 120 m. Jika energi proton sebesar $1,6\times 10^{-9}$maka induksi magnetik yang diperlukan besarnya dalam T? (UMPTN 2000)
A. 0,12
B. 0,28
C. 1,20
D. 1,60
E. 2,50
PembahasanA. 0,12
B. 0,28
C. 1,20
D. 1,60
E. 2,50
Muatan masuk dalam daerah medan magnet dengan lintasan melingkar membentuk jari - jari R
\begin{aligned}F_{L}&=F_{sp}\\ Bqv&=\frac{mv^{2}}{R}\\ R&=\frac{mv}{Bq}\end{aligned}
dengan $E_{k}=\frac{1}{2}mv^{2}$
maka $v=\sqrt{\frac{2E_{k}}{m}}$Medan magnet
\begin{aligned}B&=\frac{m}{qR}\sqrt{\frac{2E_{k}}{m}}\\ B&=\frac{1}{qR}\sqrt{2mE_{k}}\\ B&=\frac{1}{(1,6\times 10^{-19})(120)}\sqrt{2(1,67\times 10^{-27})(1,6\times 10^{-19})}\\ B&=0,12\;T\end{aligned}
Jawaban A
9. Soal
B. $2,4 \times 10^{-20}\;N$
C. $3,2\times 10^{-19}\;N$
D. $4,2\times 10^{-19}\;N$
E. $5,0\times 10^{-19}\;N$
Pembahasan
10. Soal
A. $\displaystyle \frac{\mu_{o}i(R-r)}{8Rr}$, keluar bidang gambar
B. $\displaystyle \frac{\mu_{o}i(R-r)}{8Rr}$, masuk bidang gambar
Jawaban A
9. Soal
Sebuah penghantar lurus panjang dialiri arus listrik sebesar 1,5 A. Sebuah elektron bergerak dengan kecepatan $5\times 10^{4}\; m/s$ searah arus dalam penghantar, pada jarak 0,1 m dari penghantar itu. Jika muatan elektron $-1,6 \times 10^{-19}C$, maka gaya pada elektron oleh arus dalam penghantar itu adalah? (UMPTN 2001)
A. $1,5\times 10^{-20}\;N$B. $2,4 \times 10^{-20}\;N$
C. $3,2\times 10^{-19}\;N$
D. $4,2\times 10^{-19}\;N$
E. $5,0\times 10^{-19}\;N$
Pembahasan
muatan bergerak di sekitar kawat berarus listrik akan dipengaruhi medan magnet yang timbul akibat kawat berarus listrik
Gaya Lorentz
\begin{aligned}F_{L}&=Bqv\\ F_{L}&=\frac{\mu_{o}I}{2\pi a}qv\\ F_{L}&=\frac{4\pi \times 10^{-7}(1,5)}{2\pi (0,1)}(1,6\times 10^{-19})(5\times 10^{4})\\ F_{L}&=2,4\times 10^{-20}N\end{aligned}
Jawaban B10. Soal
Seutas kawat penghantar dibentuk seperti pada gambar. Bagian yang melengkung merupakan seperempat lingkaran. Hitung medan magnet di titik A yang merupakan titik pusat lingkaran. Tentukan arahnya. (UM UGM 2015)
B. $\displaystyle \frac{\mu_{o}i(R-r)}{8Rr}$, masuk bidang gambar
C. $\displaystyle \frac{\mu_{o}i}{8(R-r)}$, keluar bidang gambar
D. $\displaystyle \frac{\mu_{o}i}{8(R-r)}$, masuk bidang gambar
E. nol
Pembahasan
Berdasarkan gambar dibagi menjadi kawat melingkar
$a_{1}>a_{2}$
$B_{1}<B_{2}$
maka:
Pembahasan
Berdasarkan gambar dibagi menjadi kawat melingkar
Diketahui
$N_{1}=N_{2}=\frac{1}{4}$
$I_{1}=I_{2}=i$$a_{1}>a_{2}$
$B_{1}<B_{2}$
maka:
\begin{aligned}B_{total}&=B_{2}-B_{1}\\ B_{total}&=\frac{\mu_{o}I_{2}}{2a_{2}}-\frac{\mu_{o}I_{1}}{2a_{1}}N_{1}\\ B_{total}&=\frac{\mu_{o}i}{2}N\left(\frac{1}{a_{2}}-\frac{1}{a_{1}}\right)\\ B_{total}&=\frac{\mu_{o}i}{2}\frac{1}{4}\left(\frac{1}{r}-\frac{1}{R}\right)\\ B_{total}&=\frac{\mu_{o}i}{8}\left(\frac{R-r}{Rr}\right)\end{aligned}
arah mengikuti medan magnet yang besar yaitu masuk bidang gambar
Jawaban B
11. Soal
$\displaystyle t=2T=\frac{4\pi m}{Bq}$
Komponen Vertikal
Jawaban B
11. Soal
Sebuah partikel bermassa m dan bermuatan q mula - mula berada di atas titi A di atas permukaan meja. Pada ruang di atas permukaan meja itu terdapat medan magnet seragam berarah vertikal ke bawah. Pada saat $t_{o}$ partikel diberi kecepatan awal dengan komponen vertikal $u_{o}$ dan mendatar $v_{o}$. Akibatnya partikel akan bergerak dengan lintasan berupa spiral vertikal ke atas. Berapakah ketinggian partikel itu diukur dari permukaan meja ketika untuk kedua kalinya partikel itu berada di atas titik A? (UM UGM 2015)
A. $\displaystyle \frac{m\pi}{qB}(v_{o}+u_{o})$
B. $\displaystyle 4\frac{m\pi}{qB}(v_{o}+u_{o})$
C. $\displaystyle 2\frac{m\pi}{qB}u_{o}$
D. $\displaystyle 4\frac{m\pi}{qB}u_{o}$
E. $\displaystyle 4\frac{m\pi}{qB}v_{o}$
Pembahasan
Pembahasan
Komponen Horizontal
\begin{aligned}F_{L}&=F_{sp}\\ Bqv&=m\omega^{2}R\\ Bq\omega R&=m\omega^{2}R\\ \omega&=\frac{Bq}{m}\\ \frac{2\pi}{T}&=\frac{Bq}{m}\\ T&=\frac{2\pi m}{Bq}\end{aligned}
Waktu untuk melakukan 2 kali putaran t = 2T$\displaystyle t=2T=\frac{4\pi m}{Bq}$
Komponen Vertikal
\begin{aligned}h&=u_{o}t\\ h&=u_{o}\left(\frac{4\pi m}{Bq}\right)\\ h&=\frac{4\pi m}{qB}u_{o}\end{aligned}
Jawaban D
12. Soal
A. $\displaystyle B=\sqrt{\frac{2mK}{e^{2}d^{2}}}$
B. $\displaystyle B=\sqrt{\frac{mK}{2e^{2}d^{2}}}$
C. $\displaystyle B=\sqrt{\frac{mK}{4e^{2}d^{2}}}$
D. $\displaystyle B=\sqrt{\frac{mK}{8e^{2}d^{2}}}$
E. $\displaystyle B=\sqrt{\frac{mK}{16e^{2}d^{2}}}$
Pembahasan
15. Soal
Dua buah kawat $i_{1}=10\;A$ dan $i_{2}=\frac{5}{\pi}$ seperti pada gambar. Besar medan magnetik pada titik P yang terletak pada pusat kawat setengah lingkaran berjari - jari 2 cm adalah?
A. $1,5\times 10^{-5}T$
B. $2,5\times 10^{-5}T$
C. $5,0\times 10^{-5}T$
D. $7,5\times 10^{-5}T$
E. $8,0\times 10^{-5}T$
Pembahasan
Kawat 2 adalah kawat melingkar dengan $N =\frac{1}{2}$ dan $a_{2}=2\times 10^{-2}m$
Jawaban D
12. Soal
Kawat berarus berada di dalam medan magnet sepanjang 50 cm. Arah kawat tegak lurus terhadap medan magnet. Ketika kawat dialiri arus 10 A, resultan gaya pada kawat terukur sebesar 3 N. Berapakah kuat medan magnet yang mempengaruhi kawat berarus itu? (UTUL UGM 2019)
A. $1,8\times 10^{-3}T$
B. $4,4\times 10^{-2}T$
C. $0,6\;T$
D. $1,4\; T$
E. $5,2\; T$
Pembahasan
Pembahasan
Diketahui
$l= 50 \;cm =5\times 10^{-1}\;m$
$I=10\;A$
$F=3\;N$
Medan Magnetik (B)?
$l= 50 \;cm =5\times 10^{-1}\;m$
$I=10\;A$
$F=3\;N$
Medan Magnetik (B)?
\begin{aligned}F&=BIl\\ 3&=B(10)(5\times 10^{-1})\\ B&=\frac{3}{5}\\ B&=0,6\; Tesla\end{aligned}
Jawaban C
13. Soal
Jawaban C
13. Soal
Kumparan kawat P memiliki 10 lilitan dan kumparan kawat Q memiliki 30 lilitan diletakkan sepusat. Gambar berikut menunjukkan kedua kumparan tampak dari atas.
Kumparan P berjari - jari 5 cm dan kumparan Q berjari - jari 20 cm. Kuat arus yang mengalir pada kumparan Q adalah $I_{Q}=20\;A$, dan resultan kuat medan magnet di pusat lingkaran adalah nol. Berapakah kuat arus yang mengalir di kawat P ($I_{P}$) ? (UN 2019)
A. 15 A
B. 20 A
C. 25 A
D. 30 A
E. 35 A
Pembahasan
Diketahui
Gambar
Medan Magnet
$I_{Q}=20\;A$
$a_{p}=5\;cm=5\times 10^{-2}m$
$a_{q}=20\;cm=20\times 10^{-2}m$
14. Soal
$I_{Q}=20\;A$
$a_{p}=5\;cm=5\times 10^{-2}m$
$a_{q}=20\;cm=20\times 10^{-2}m$
Kuat medan magnet di pusat nol, maka:
\begin{aligned}B_{p}&=B_{q}\\ \frac{\mu_{o}I_{p}}{2a_{p}}N_{p}&=\frac{\mu_{o}I_{q}}{2a_{q}}N_{q}\\ \frac{I_{p}}{a_{p}}N_{p}&=\frac{I_{q}}{a_{q}}N_{q}\\ \frac{I_{p}}{5}(1)&=\frac{20}{20}(30)\\ I_{p}&=15\;A\end{aligned}
Jawaban A14. Soal
Sebuah elektron (e) bermassa m bergerak dengan energi kinetik K tidak akan menumbuk lempeng berjarak d dari tempat mulai elektron bergerak jika medan magnet diberikan dipermukaan lempeng. Besar medan magnet tersebut adalah (SIMAK UI 2012)
B. $\displaystyle B=\sqrt{\frac{mK}{2e^{2}d^{2}}}$
C. $\displaystyle B=\sqrt{\frac{mK}{4e^{2}d^{2}}}$
D. $\displaystyle B=\sqrt{\frac{mK}{8e^{2}d^{2}}}$
E. $\displaystyle B=\sqrt{\frac{mK}{16e^{2}d^{2}}}$
Pembahasan
Diketahui
$Ek = K$
$q = e$
$R = d$
muatan bergerak membentuk lintasan melingkar maka v dan B saling tegak lurus
\begin{aligned}F_{L}&=F_{sp}\\ Bqv&=\frac{mv^{2}}{R}\\ B&=\frac{mv}{Rq}\end{aligned}
karena
\begin{aligned}E_{k}=\frac{1}{2}mv^{2}\\ v&=\sqrt{\frac{2E_{k}}{m}}\\ v&=\sqrt{\frac{2K}{m}}\end{aligned}
disubtitusi ke persamaan medan magnet
Jawaban A\begin{aligned}B&=\frac{mv}{Rq}\\ B&=\frac{m}{Rq}\sqrt{\frac{2K}{m}}\\ B&=\sqrt{\frac{2mK}{R^{2}q^{2}}}\\ B&=\sqrt{\frac{2mK}{R^{2}e^{2}}}\\ B&=\sqrt{\frac{2mK}{e^{2}d^{2}}}\end{aligned}
15. Soal
Dua buah kawat $i_{1}=10\;A$ dan $i_{2}=\frac{5}{\pi}$ seperti pada gambar. Besar medan magnetik pada titik P yang terletak pada pusat kawat setengah lingkaran berjari - jari 2 cm adalah?
A. $1,5\times 10^{-5}T$
B. $2,5\times 10^{-5}T$
C. $5,0\times 10^{-5}T$
D. $7,5\times 10^{-5}T$
E. $8,0\times 10^{-5}T$
Pembahasan
Diketahui
Dua kawat $i_{1}=10\;A$ dan $i_{2}=\frac{5}{\pi}$
Kawat 1 adalah kawat lurus dengan $a_{1}=2\times 10^{-2}m$
\begin{aligned}B_{1}=\frac{\mu_{o}i_{1}}{2\pi a_{1}}\\ B_{1}&=10\times 10^{-5}T\end{aligned}Dua kawat $i_{1}=10\;A$ dan $i_{2}=\frac{5}{\pi}$
Kawat 2 adalah kawat melingkar dengan $N =\frac{1}{2}$ dan $a_{2}=2\times 10^{-2}m$
\begin{aligned} B_{2}&=\frac{\mu_{o}i_{2}}{2a_{2}}N\\ B_{2}&=\frac{4\pi \times 10^{-7}(\frac{5}{\pi})}{2(2\times 10^{-2})}\frac{1}{2}\\ B_{2}&=2,5\times 10^{-5}T\end{aligned}
karena arah medan magnet berlawanan arah maka saling meniadakan
$B_{total}=(10-2,5)\times 10^{-5}T$
$B_{total}=7,5\times 10^{-5}T$ masuk bidang gambar
Jawaban D
16. Soal
karena arah medan magnet berlawanan arah maka saling meniadakan
$B_{total}=(10-2,5)\times 10^{-5}T$
$B_{total}=7,5\times 10^{-5}T$ masuk bidang gambar
Jawaban D
16. Soal
Sebuah kawat dibentuk menjadi lingkaran dengan diameter 12 cm, kemuidan diberi arus listrik sebesar 2 A. Berapakah besar induksi magnetik pada titik sumbu lingkaran yang berada pada jarak 8 cm dari pusat lingkaran. (SIMAK UI 2010)
A. $2,4\mu \;Weber$
B. $3,6\mu \;Weber$
C. $4,8\mu \;Weber$
D. $5,0\mu \;Weber$
E. $6,2\mu \;Weber$
medan magnet titik di perpanjangan sumbu putarB. $3,6\mu \;Weber$
C. $4,8\mu \;Weber$
D. $5,0\mu \;Weber$
E. $6,2\mu \;Weber$
Pembahasan
Diketahui
Kawat melingkar
maka nilai $sin\; \theta=\frac{6}{10}=\frac{3}{5}$
Kawat melingkar
\begin{aligned}B&=\frac{\mu_{o}I}{2a}N\,sin^{3}\theta\\ B&=\frac{\mu_{o}(2)}{2(6\times 10^{-2})}(1)\left(\frac{3}{5}\right)^{3}\\ B&=3,6\mu_{o}\; Weber\end{aligned}
Jawaban B
17. Soal
Jawaban B
17. Soal
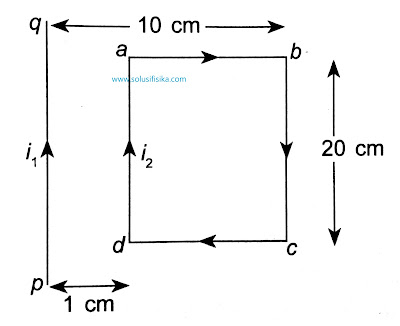
Pada gambar berikut terlukis bahwa kawat panjang pq dilalui arus listrik $i=10\;A$ dan kawat empat persegi panjang $i_{2}=5A$. Resultan gaya dialami kawat empat persegi panjang abcd (dalam mikronewton) ? (UMPTN 1994)
A. 20
B. 60
C. 120
D. 180
E. 220
Pembahasan
Diketahui
$i_{1}=10\;A$
$i_{2}=5\;A$ (abcd)
$l=20\; cm = 0,2\; m$
kawat ad
$a_{ad}=1\;cm=1\times 10^{-2}m$
kawat bc$a_{bc}=10\;cm=10\times 10^{-2}m$
Kawat ad dengan kawat pq arah arus listrik searah maka timbul gaya lorentz tarik menarik
Kawat ad dengan kawat pq arah arus listrik searah maka timbul gaya lorentz tarik menarik
\begin{aligned}F_{ad}&=\frac{\mu_{o}i_{1}i_{2}}{2\pi a_{ad}}l\\ F_{ad}&=\frac{4\pi \times (10)(5)}{2\pi(1\times 10^{-2})}(20\times 10^{-2})\\ F_{ad}&=200\times 10^{-6}N\end{aligned}
Kawat bc dengan kawat pq arah arus listrik berlawanan maka timbul gaya lorentz tolak menolak
Kawat bc dengan kawat pq arah arus listrik berlawanan maka timbul gaya lorentz tolak menolak
\begin{aligned}F_{bc}&=\frac{\mu_{o}i_{1}i_{2}}{2\pi a_{bc}}l\\ F_{bc}&=\frac{4\pi \times (10)(5)}{2\pi(10\times 10^{-2})}(20\times 10^{-2})\\ F_{bc}&=20\times 10^{-6}N\end{aligned}
Gaya total yang dialami kawat abcd
karena arah gaya berlawanan maka:
Gaya total yang dialami kawat abcd
karena arah gaya berlawanan maka:
$F_{abcd}=F_{total}=(200-20)\times 10^{-6}=180\times 10^{6}N\\ F_{abcd}=F_{total}=180\; \mu N$
Jawaban D
18. Soal
Sebuah arus terbagi dua seperti ditunjukkan pada gambar. Berapa induksi magnetik (besar dan arah ) dipusat P dari lingkaran berjari - jari a?
A. $\displaystyle B=\frac{3}{2}\frac{\mu_{o}i}{a}$
B. $\displaystyle B=\frac{2}{3}\frac{\mu_{o}i}{a}$
C. $\displaystyle B=\frac{1}{2}\frac{\mu_{o}i}{a}$
D.$\displaystyle B=\frac{3}{8}\frac{\mu_{o}i}{a}$
E.$\displaystyle B=\frac{1}{8}\frac{\mu_{o}i}{a}$
Pembahasan
Diketahui
kawat melingkar
Jawaban D
18. Soal
Sebuah arus terbagi dua seperti ditunjukkan pada gambar. Berapa induksi magnetik (besar dan arah ) dipusat P dari lingkaran berjari - jari a?
A. $\displaystyle B=\frac{3}{2}\frac{\mu_{o}i}{a}$
B. $\displaystyle B=\frac{2}{3}\frac{\mu_{o}i}{a}$
C. $\displaystyle B=\frac{1}{2}\frac{\mu_{o}i}{a}$
D.$\displaystyle B=\frac{3}{8}\frac{\mu_{o}i}{a}$
E.$\displaystyle B=\frac{1}{8}\frac{\mu_{o}i}{a}$
Pembahasan
Diketahui
kawat melingkar
$I_{1}=\frac{3}{4}i$
$I_{2}=\frac{1}{4}i$
$N_{1}=N_{2}=\frac{1}{2}\;lilitan$
$a_{1}=a_{2}=a$
kawat 1 arah B masuk bidang
kawat 2 arah B keluar bidang
$I_{2}=\frac{1}{4}i$
$N_{1}=N_{2}=\frac{1}{2}\;lilitan$
$a_{1}=a_{2}=a$
kawat 1 arah B masuk bidang
kawat 2 arah B keluar bidang
$B_{1}=\frac{\mu_{o}I_{1}}{2a_{1}}N=\frac{\mu_{o}\frac{3}{4}i}{2a}\left(\frac{1}{2}\right)=\frac{3}{16}\frac{\mu_{o}i}{a}$
$B_{2}=\frac{\mu_{o}I_{1}}{2a_{2}}N=\frac{\mu_{o}\frac{1}{4}i}{2a}\left(\frac{1}{2}\right)=\frac{1}{16}\frac{\mu_{o}i}{a}$
karena arah medan magnet berlawanan, maka:
$B_{2}=\frac{\mu_{o}I_{1}}{2a_{2}}N=\frac{\mu_{o}\frac{1}{4}i}{2a}\left(\frac{1}{2}\right)=\frac{1}{16}\frac{\mu_{o}i}{a}$
karena arah medan magnet berlawanan, maka:
\begin{aligned}B_{total}&=B_{1}-B_{2}\\ B_{total}&=\left(\frac{3}{16}-\frac{1}{16}\right)\frac{\mu_{o}i}{a}\\ B_{total}&=\frac{1}{8}\frac{\mu_{o}i}{a}\end{aligned} masuk bidang
Jawaban E
19. Soal
Jawaban E
19. Soal
Kawat berarus berada di dalam medan magnet sepanjang 50 cm. Arah kawat tegak lurus terhadap medan magnet. Ketika kawat dialiri arus 10 A, resultan gaya pada kawat terukur sebesar 3 N. Berapakah kuat medan magnet yang mempengaruhi kawat berarus itu? (UTUL UGM 2019)
A. $1,8\times 10^{-3}C$
B. $4,4\times 10^{-2}C$
C. $0,6\;T$
D. $1,4\;T$
E. $5,2\;T$
Pembahasan
Diketahui
$l=50\; cm =5 \times 10^{-1}m$
$I= 10\; A$
$F= 3\; N$
Medan Magnetik (B)?
Diketahui
$l=50\; cm =5 \times 10^{-1}m$
$I= 10\; A$
$F= 3\; N$
Medan Magnetik (B)?
\begin{aligned}F&=BIl\\ 3&=B(10)(5\times 10^{-1})\\ B&=\frac{3}{5}\\ B&=0,6\; Tesla\end{aligned}
Jawaban C
Jawaban C
20. Soal
Proyeksi gerak sebuah partikel bermuatan negatif -q kekanan dan bermassa m pada bidang xy tampak pada gambar di atas. Di ruang itu terdapat medan magnet tetap B searah sumbu z positif, tidak ada medan listrik E dan komponen kecepatan $v_{x} > 0$. Komponen kecepatan pada bidang xy dan v adalah?(UTBK 2021)
A. $\displaystyle \frac{qBR}{m}$ searah gerak jarum jam dan $v_{x}$ konstan
B. $\displaystyle \frac{qBR}{m}$ searah gerak jarum jam dan $v_{x}$ tidak konstan
C. $\displaystyle \frac{qBm}{R}$ berlawanan arah gerak jarum jam dan $v_{x}$ konstan
D. $\displaystyle \frac{qBm}{R}$ berlawanan arah gerak jarum jam dan $v_{x}$ tidak konstan
B. $\displaystyle \frac{qBR}{m}$ berlawanan arah gerak jarum jam dan $v_{x}$ konstan
B. $\displaystyle \frac{qBR}{m}$ berlawanan arah gerak jarum jam dan $v_{x}$ konstan
Pembahasan
Gaya Lorentz
Muatan masuk dalam daerah medan magnet membentuk lintasan melingkar
berlaku:
\begin{aligned}F_{L}&=F_{sp}\\ Bqv&=\frac{mv^{2}}{R}\\ v_{x}&=\frac{qBR}{m}\end{aligned}
Kaidah tangan kanan 2
$B\to Z(+)$
$F\to Y(+)$
$v\to X(+)$
nilai kecepatan linear tetap dan arah berubah
Jawaban D
Tags:
Listrik Magnet
