Pembahasan Soal Pemuaian

Solusi Soal Pemuaian Panjang, Luas dan Volume

1. Soal

Sebuah drum terbuat dari besi (koefisien muai panjang besi adalah $12\times 10^{-6}/^{\circ}C$) volumenya 200 liter diisi minyak tanah sampai penuh (koefisien muai volume minyak $936\times 10^{-6}/^{\circ}C$) diletakkan di halaman toko pengecer minyak di pagi hari saat suhunya $25^{\circ}C$. Pada siang hari suhu naik menjadi $35^{\circ}C$, bila drum tidak ditutup dan minyak dianggap tidak menguap maka volume minyak yang tumpah akibat pemuaian adalah sekitar (UM UNDIP 2010)
A. 3,6 liter
B. 2,6 liter
C. 1,8 liter
D. 1,6 liter
E. 1,2 liter
Pembahasan
Volume awal wadah dan minyak sama (penuh)
$V_{o(zc)}=V_{o(wadah)}=V_{o}=200\;liter$
maka:
\begin{aligned}V_{tumpah}&=V_{o}\Delta T(\gamma_{zc}-3\alpha_{wadah})\\ V_{tumpah}&=200(35-25)(936-3(12))\times 10^{-6}\\ V_{tumpah}&=2000(900)\times 10^{-6}\\ V_{tumpah}&=1,8\; liter\end{aligned}

Jawaban C

2. Soal

Grafik pertambahan panjang sebuah kawat sebagai fungsi pertambahan suhu dilukiskan oleh gambar berikut

Bila panjang mula - mula kawat pada suhu $0^{\circ}C$ sama dengan 10 m, maka koefisien linear muai panjangnya sama dengan ... (UM UNDIP 2012)
A. $10^{-2}/^{\circ}C$
B. $10^{-3}/^{\circ}C$

C. $10^{-4}/^{\circ}C$

D. $10^{-5}/^{\circ}C$

E. $10^{-6}/^{\circ}C$

Pembahasan

Pemuaian panjang
\begin{aligned} \Delta L&=L_{o}\alpha \Delta T\\10&=10\alpha (100)\\ \alpha&=10^{-2}/^{\circ}C\end{aligned}

Jawaban A

3. Soal

Sebatang rel kereta api memiliki panjang 30 m ketika suhu $30^{\circ}C$, untuk menguji sifat termal rel tersebut, maka dilakukan percobaan dengan menaikkan suhunya menjadi $45^{\circ}C$ sehingga panjangnya menjadi 30,0075 m. Jika rel diuji pada suhu $5^{\circ}C$, maka panjangnya menjadi (SBMPTN 2013)

A. 29,8875 m

B. 28,9875 m

C. 29,9950 m

D. 29,9925 m

E. 29,9900 m

Pembahasan

Keadaan Pertama (1)

$\Delta L_{1}=30,0075-30=0,0075\;m$

$\Delta T_{1}=45-30=15^{\circ}C$

Keadaan Kedua (2)

$\Delta L_{2}=L_{2}-30$

$\Delta T_{2}=5-30=-25^{\circ}C$

karena rel kereta api yang sama maka nilai panjang mula -mula dan  koefisien muai panjang $\alpha$ sama

berdasarkan rumus $\Delta L=L_{o}\alpha \Delta T$

diperoleh

\begin{aligned}\frac{\Delta L_{1}}{\Delta L_{2}}&=\frac{\Delta T_{1}}{\Delta_{2}}\\ \frac{0,0075}{L_{2}-30}&=\frac{15}{-25}\\ L_{2}&=29,9875\end{aligned}

Jawaban B

4. Soal

Sebuah tangki baja yang memiliki koefisien muai panjang $12\times 10^{-6}/^{\circ}C$dan bervolume $0,05\;m^{3}$ diisi penuh dengan bensin yang memiliki koefisien muai ruang $950\times 10^{-6}/^{\circ}C$ pada temperatur $20^{\circ}C$. Jika kemudian tangki ini dipanaskan sampai 50 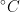 maka jumlah bensin yang tumpah adalah sebanyak? (SPMB 2006)

A. $457\times 10^{-6}\; m^{3}$

B. $914\times 10^{-6}\; m^{3}$

C. $1371\times 10^{-6}\; m^{3}$

D. $1828\times 10^{-6}\; m^{3}$

E. $2285\times 10^{-6}\; m^{3}$

Pembahasan

Karena wadah berisi penuh zat cair maka 

$V_{o(wadah)}=V_{o(zc)}=V_{o}$

maka

\begin{aligned}V_{tumpah}&=V_{o}\Delta T (\gamma_{zc}-3\alpha_{wadah})\\ V_{tumpah}&=0,05 \times (50-20)(950-36) \times 10^{-6}\\ V_{tumpah}&=1371\times 10^{-6}\end{aligned}

Jawaban C
5. Soal
Sebuah cangkir silinder terbuat dari tembaga berisi penuh air pada suhu $20,0^{\circ}C$ . Jika cangkir berisi air tersebut dipanaskan hingga $91,0^{\circ}C$, berapa banyak air yang tumpah? Dikahui koefisien muai linear tembaga adalah $16\times 10^{-6}/^{\circ}C$ dan koefisien muai volume air adalah $207\times 10^{-6}/^{\circ}C$. (SBMPTN 2013)
A. 0,1 %
B. 1,1 %
C. 0,2 %
D. 2,2 %
E. 0,3 %
Pembahasan
Karena wadah berisi penuh maka:
\begin{aligned}V_{tumpah}&=V_{o}\Delta T(\gamma_{zc}-3\alpha_{wadah})\\ V_{tumpah}&= V_{o}(91-20)(207-3(16))\times 10^{-6}\\ V_{tumpah}&=V_{o}(71)(159)\times 10^{-6}\\ V_{tumpah}&=0,0113V_{o}\end{aligned}

Persentase banyak air yang tumpah

$\displaystyle \frac{V_{tumpah}}{V_{o}}=0,0113$

$\displaystyle \frac{V_{tumpah}}{V_{o}}=1,13% $
Jawaban B
6. Soal

Untuk menambahkan panjang kawat logam dari 50,0 mm menjadi 50,1 mm, temperatur cincin harus dinaikkan sebesar $80^{\circ}C$. Perubahan temepratur yang diperlukan untuk menambah panjang sebuah kawat logam yang sama daru 100,00 mm menjadi 100,1 mm adalah? (SNMPTN 2011)

A. $20^{\circ}C$
B. $40^{\circ}C$
C. $80^{\circ}C$
D. $120^{\circ}C$
E. $160^{\circ}C$
Pembahasan

Kawat logam sama maka nilai koefisien muai panjangnya ($\alpha$)  juga sama  

Keadaan 1

$\Delta L_{1}=50,1-50,0=0,1\;mm$
$\Delta T_{1}=80^{\circ}C$
Keadaan 2
$\Delta L_{2}=100,1-100,0=0,1\;mm$
$\Delta T_{2}=. . . . ?$
maka:

\begin{aligned} \frac{\Delta L_{1}}{\Delta L_{2}}&=\frac{L_{o1} \Delta T_{1}}{L_{o2} \Delta T_{2}}\\ \frac{0,1}{0,1}&=\frac{50.80}{100.\Delta T_{2}}\\ \Delta T_{2}&=40^{\circ}C\end{aligned}

Jawaban B
7. Soal

Sebuah kubus dengan volume V terbuat dari bahan yang koefisien muai panjangnya $\alpha$ . Jika suhu kubus dinaikkan sebesar $\Delta T$ , maka luasnya akan bertambah sebesar? (SPMB 2004)

A. $\alpha V \Delta T$

B. $6\alpha V \Delta T$

C. $12\alpha V \Delta T$

D. $6\alpha V^{2/3} \Delta T$

E. $12\alpha V^{2/3} \Delta T$

Pembahasan

Kubus

$V=s^{3}$ maka $s=V^{\frac{1}{3}}$

$A=6s^{2}$

$A=6V^{\frac{2}{3}}$

maka

\begin{aligned} \Delta A&=A\beta \Delta T\\ \Delta A&=6V^{\frac{2}{3}}2\alpha \Delta T\\ \Delta A&=12\alpha V^{\frac{2}{3}}\Delta T\end{aligned}

Jawaban E

8. Soal

Sebuah kubus dengan koefisien muai panjang $\alpha$ mula - mula memiliki volume $V_{o}$. Setelah dipanaskan pertambahan luasnya adalah $\Delta A$. Kenaikan suhu kubus adalah (UTUL UGM 2017)

A. $\displaystyle \frac{1}{16}\Delta A V_{o}^{-\frac{2}{3}}\alpha^{-1}$

B. $\displaystyle \frac{1}{12}\Delta A V_{o}^{-\frac{2}{3}}\alpha^{-1}$

C. $\displaystyle \frac{1}{8}\Delta A V_{o}^{-\frac{2}{3}}\alpha^{-1}$

D. $\displaystyle \frac{1}{6}\Delta A V_{o}^{-\frac{2}{3}}\alpha^{-1}$

E. $\displaystyle \frac{1}{4}\Delta A V_{o}^{-\frac{2}{3}}\alpha^{-1}$

Pembahasan

Kubus

$V=s^{3}$ maka $s=V^{\frac{1}{3}}$

$A=6s^{2}$

$A=6V^{\frac{2}{3}}$

maka

\begin{aligned} \Delta A&=A\beta \Delta T\\ \Delta A&=6V^{\frac{2}{3}}2\alpha \Delta T\\ \Delta A&=12\alpha V^{\frac{2}{3}}\Delta T\\ \Delta T&=\frac{1}{2}\Delta AV_{o}^{-\frac{2}{3}}\alpha^{-1}\end{aligned}

Jawaban B

9. Soal

Sebatang rel kereta api memiliki panjang 30 m ketika suhu $20^{\circ}C$, untuk menguji sifat termal rel tersebut, maka dilakukan percobaan dengan menaikkan suhunya menjadi $40^{\circ}C$ sehingga panjangnya menjadi 30,0075 m. Jika rel diuji pada suhu $-10^{\circ}C$ , maka panjangnya menjadi (SBMPTN 2013)

A. 29,97250 m

B. 28,97750 m

C. 29,98250 m

D. 29,98750 m

E. 29,98875 m

Pembahasan

Keadaan Pertama (1)

$\Delta L_{1}=30,0075-30=0,0075\;m$

$\Delta T_{1}=40-20=20^{\circ}C$

Keadaan Kedua (2)

$\Delta L_{2}=L_{2}-30$

$\Delta T_{2}=-10-20=-30^{\circ}C$

karena rel kereta api yang sama maka nilai panjang mula -mula dan  koefisien muai panjang  sama

berdasarkan rumus $\Delta L=L_{o}\alpha \Delta T$

diperoleh

\begin{aligned} \frac{\Delta L_{1}}{\Delta L_{2}}&=\frac{\Delta T_{1}}{\Delta T_{2}}\\ \frac{0,0075}{L_{2}-30}&=\frac{20}{-30}\\ L_{2}&=29,98875\; m\end{aligned}

Jawaban E

10. Soal

Sebatang tembaga dipanaskan sampai  $300^{\circ}C$ lalu dijepit dengan kuat sehingga tidak dapat menyusut ketika suhunya turun. Diketahui Modulus Young tembaga $110\times 10^{9}N/m^{2}$ dan koefisien muai panjang  $15\times 10^{-6}/K$. Jika tegangan patahnya sebesar $220\times 10^{6}N/m^{2}$ dan suhunya diturunkan, batang akan mulai putus pada suhu? (SPMB 2004)
A. $100\; ^{\circ}C$
B. $123\; ^{\circ}C$

C. $155\; ^{\circ}C$

D. $167\; ^{\circ}C$

E. $300\; ^{\circ}C$

Pembahasan

$\displaystyle E=\frac{\sigma}{e}=\frac{tegangan}{regangan}$

\begin{aligned}e&=\frac{\sigma}{E}\\ \frac{\Delta L}{L}&=\frac{\sigma}{E}\\ \frac{L\alpha \Delta T}{L}&=\frac{\sigma}{E}\\ \Delta T&= \frac{\sigma}{\alpha E}\\ \Delta T&=\frac{220\times 10^{6}}{15\times 10^{-6}\times 110\times 10^{9}}\\ \Delta T&=\frac{400}{3}^{\circ}C\end{aligned}

maka:

\begin{aligned} \Delta T&=-\frac{400}{3}\\ T_{2}&=T_{1}+\Delta T\\ T_{2}&=300+\left(-\frac{400}{3}\right)\\ T_{2}&=167^{\circ}C\end{aligned}

Jawaban D