Solusi Soal Usaha dan Energi
1. Soal
Benda bermassa 2 kg dari keadaan diam dipercepat oleh gaya konstan sebesar 2 N. Berapa waktu yang diperlukan oleh gaya tersebut sehingga benda bergerak dengan kinetik 100 J. (UM UGM 2016)
A. 2 s
B. 4 s
C. 6 s
D. 8 s
E. 10 s
Pembahasan
Diketahui
$v_{o}=0\;m/s$
$m=2\;kg$
$F=2\;N$
$Ek_{t}=100\;joule$
Gaya dorong (F)
\begin{aligned} F&=ma\\ a&=\frac{F}{m}\\ a&=\frac{1}{2}\\ a&=1\;m/s^{2} \end{aligned}
Jarak (S)
\begin{aligned} s&=v_{o}t+\frac{1}{2}at^{2}\\ s&=0+\frac{1}{2}at^{2}\end{aligned}
Usaha
\begin{aligned} W&=\Delta E_{k}\\ F.s&=E_{k(t)}-E_{k(o)}\\ F.\frac{1}{2}at^{2}&=E_{k(t)}\\ (2)\frac{1}{2}(1)t^{2}&=100\\ t&=10\;s \end{aligned}
Jawaban E
2. Soal
Sebuah pegas dari suatu pistol mainan anak - anak adalah 100 N/m. Sebelum ditembakkan dengan arah vertikal ke atas, peluru 10 gram mampu menekan pegas 20 cm. Ketinggian maksimum yang dicapai peluru setelah ditembakkan adalah? (UMPTN 1991)
A. 10 m
B. 20 m
C. 40 m
D. 60 m
E. 80 m
Pembahasan
k = 100 N/m
x = 20 cm = 0,2 m
m = 10 gram = 0,01 kg
Tinggi maksimum?
Energi potensial pegas diubah menjadi energi potensial benda
\begin{aligned} E_{p(pegas)}&=E_{p(benda)}\\ \frac{1}{2}kx^{2}&=m_{b}gh\\ h&=\frac{1}{2}\frac{kx^{2}}{m_{b}g}\\ h&=\frac{1}{2}\frac{(100)(0,2)^{2}}{(10\times 10^{-3})(10)}\\ h&=20\; m\end{aligned}
Jawaban
B
3. Soal
Dua buah benda masing - masing memiliki massa A kg dan B kg. Jika kedua benda mula - mula diam, kemudian mengalami gaya yang sama besarnya dan dalam selang waktu yang sama maka perbandingan energi kinetik benda A dan benda B tepat pada akhir waktu yang diberikan gaya adalah? (SPMB 2004)
A. $1$
B. $\displaystyle \frac{B}{A}$
C. $\displaystyle \frac{A}{B}$
D. $\displaystyle \left(\frac{B}{A} \right)^{2}$
E. $\displaystyle \left(\frac{A}{B} \right)^{2}$
Pembahasan
Diketahui
$m_{1}=A$
$m_{2}=B$
karena $F_{1}=F_{2}=F$ dan $t_{1}=t_{2}=t$ maka nilai momentum benda 1 dan benda kedua sama $p_{1}=p_{2}=p$
Energi Kinetik
$\displaystyle E_{k}=\frac{1}{2}mv^{2}=\frac{1}{2}\frac{p^{2}}{m}$
maka:
$\displaystyle \frac{E_{k1}}{E_{k2}}=\frac{m_{2}}{m_{1}}$
$\displaystyle \frac{E_{k2}}{E_{k3}}=\frac{B}{A}$
Jawaban B
4. Soal
Massa 1 kg bergetar selaras sederhana pada sistem pegas dengan tetapan gaya k = 400 N/m. Jika amplitudo getaran tersebut 5 cm, berapa kecepatan massa tersebut pada saat melewati titik seimbang? (UM UGM 2013)
A. 8 m/s
B. 4 m/s
C. 2 m/s
D. 1 m/s
E. 0,5 m/s
Pembahasan
Diketahui
m = 1 kg
k = 400 N/m
A = 5 cm = 0,05 m
Energi potensial pegas menjadi energi kinetik pegas dititik seimbang.
\begin{aligned} E_{p(pegas)}&=E_{k(pegas)}\\ \frac{1}{2}kA^{2}&=\frac{1}{2}mv^{2}\\ v&=A\frac{k}{m}\\ v&=(5\times 10^{-2})\sqrt{\frac{400}{1}}\\ v&=1\;m/s\end{aligned}
Jawaban
D
5. Soal
Benda dengan massa 2 kg bergerak dengan laju konstan 10 m/s, kemudian menabrak sebuah pegas yang dalam keadaan bebas sehingga tertekan sebesar 10 cm. Jika gesekan - gesekan diabaikan, maka konstanta pegas tersebut adalah
A. 11000 N/m
B. 14000 N/m
C. 17000 N/m
D. 20000 N/m
E. 24000 N/m
Pembahasan
m 2 kg
v = 10 m/s
x = 10 cm = 0,1 m
Energi kinetik benda menjadi energi potensial pegas?
\begin{aligned}Ek_{benda}&=Ep_{pegas}\\ \frac{1}{2}mv^{2}&=\frac{1}{2}kx^{2}\\ k&=\frac{mv^{2}}{x^{2}}\\ k&=\frac{(2)(10)^{2}}{(0,1)^{2}}\\ k&=20000\; N/m\end{aligned}
Jawaban
D
6. Soal
Sebuah batu dilemparkan dari tanah vertikal ke atas dengan kecepatan awal $v_{o}=\sqrt{7}$. Ketika sampai ketinggian dua kalinya, kecepatan menjadi setengahnya. Jika $g = 10\;m/s^{2}$, nilai h adalah? (UM UGM 2015)
A. $\displaystyle \frac{1}{20}m$
B. $\displaystyle \frac{1}{10}m$
C. $\displaystyle \frac{3}{20}m$
D. $\displaystyle \frac{1}{5}m$
E. $\displaystyle \frac{1}{4}m$
Pembahasan
Berlaku hukum kekekalan energi
Tinjau AB
\begin{aligned} E_{pA}+E_{kA}&=E_{pB}+E_{kB}\\ mgh^{A}+\frac{1}{2}mv_{A}^{2}&=mgh_{B}+\frac{1}{2}mv_{B}^{2}\\ 0+\frac{1}{2}v_{o}^{2}&=gh+\frac{1}{2}v^{2}\\ \frac{1}{2}v_{o}^{2}&=gh+\frac{1}{2}v^{2}\\ v_{o}^{2}&=2gh+v^{2}\end{aligned}
Tinjau AC
\begin{aligned}E_{pA}+E_{kA}&=E_{pC}+E_{kC}\\ mgh^{A}+\frac{1}{2}mv_{A}^{2}&=mgh_{C}+\frac{1}{2}mv_{C}^{2}\\ 0+\frac{1}{2}v_{o}^{2}&=gh+\frac{1}{2}(\frac{1}{2}v^{2})\\ \frac{1}{2}v_{o}^{2}&=2gh+\frac{1}{8}v^{2}\\ 4v_{o}^{2}&=16gh+v^{2}\end{aligned}
dari 2 persamanan diatas diperoleh:
\begin{aligned}4v_{o}^{2}&=16gh+v^{2}\\ v_{o}^{2}&=2gh+v^{2}\\ ---&------\;\;-\\ 3v_{o}^{2}&=14gh\\ 3(\sqrt{7})^{2}&=14(10)h\\ 21&=140h\\ h&=\frac{3}{20}\;m \end{aligned}
Jawaban
C
7. SoalSebuah benda bermassa 4 kg, mula mula diam kemudian bergerak lurus dengan percepatan $3\;m/s^{2}$,. Usaha yang diubah menjadi energi kinetik setelah 2 detik adalah? (UMPTN 1989)
A. 6 joule
B. 12 joule
C. 24 joule
D. 48 joule
E. 72 joule
Pembahasan
Diketahui
m=4 kg
t = 2 sekon
$a=3 \; m/s^{2}$
$v_{o}=2\; detik$
maka
$v_{t}=v_{o}+at$
$v_{t}=0+(3)(2)$
$v_{t}=6\;m/s$
Usaha setelah 2 sekon
\begin{aligned}W&=\Delta E_{k}\\ W&=\frac{1}{2}m(v_{t}^{2}-v_{o}^{2})\\ W&=\frac{1}{2}(4)(6^{2}-0^{2})\\ W&=72\; joule \end{aligned}
Jawaban
E
8. Soal
Dua benda A dan B yang bermassa masing - masing m, jatuh bebas dari ketinggian h meter dan 2h meter. Jika A menyentuh tanah dengan kecepatan v m/s, maka benda B akan menyentuh tanah dengan energi kinetik sebesar?
A. $\displaystyle \frac{1}{2}mv^{2}$
B. $\displaystyle mv^{2}$
C. $\displaystyle \frac{1}{4}mv^{2}$
D. $\displaystyle \frac{3}{4}mv^{2}$
E. $\displaystyle \frac{3}{2}mv^{2}$
Berlaku hukum kekekalan energi
\begin{aligned}E_{p1}+E_{k1}&=E_{p2}+E_{k2}\\ E_{p1}+0&=0+E_{k2}\\ E_{p1}&=E_{k2}\end{aligned}
Benda A dan B
\begin{aligned} \frac{E_{pA}}{E_{pB}}&=\frac{E_{kA}}{E_{kB}}\\ \frac{mgh}{mg(2h)}&=\frac{\frac{1}{2}mv^{2}}{E_{kB}}\\ E_{kB}&=mv^{2}\end{aligned}
Jawaban
B
9. Soal
Usaha yang dilakukan oleh gaya konservatif pada benda hanya bergantung pada posisi awal dan akhir benda itu saja, tidak bergantung pada lintassan yang dilaluinya
SEBAB
Gesekan membuat energi mekanik suatu benda selalu lebih kecil dari energi mekanik awal benda.
(SIMAK UI 2012)
Pembahasan
Pernyataan Benar
Usaha karena gaya konservatif tidak bergantung pada lintasan, bergantung pada posisi awal dan posisi akhir
Alasan Benar
Gesekan mengurangi nilai energi mekanik benda
Pernyataan dan alasan benar tidak berhubungan
Jawaban
B
10. Soal
Sebuah benda bermassa m diluncurkan dari dasar sebuah bidang miring dengan kecepatan awal v seperti gambar berikut. Jika koefisien gesekan kinetik adalah $\mu_{k}$, percepatan gravitasi g maka kecepatan minimum agar benda tersebut dapat mencapai puncak bidang miring adalah? (SPMB 2006)
A. $v=\sqrt{2gh}-\sqrt{2\mu_{k}gl}$
B. $v=\sqrt{2(gh-\mu_{k}gl}$
C. $v=\sqrt{2gh}$
D. $v=\sqrt{2gh}+\sqrt{2\mu_{k}gl}$
E. $v=\sqrt{2(gh-\mu_{k}gl}$
Pembahasan
Diketahui
$sin\; \theta =\frac{h}{s}$ maka $h= s\; sin\; \theta$
$cos\; \theta= \frac{l}{s}$ maka $l=s\; sin\; \theta$
Usaha (W)
\begin{aligned} W&=\Delta E_{k}\\ \Sigma F s&=\frac{1}{2}m(v_{t}^{2}-v_{o}^{2})\\ (-mg sin\; \theta -f_{g})s&=\frac{1}{2}m(v_{t}^{2}-v_{o}^{2})\\ -(mg\;sin\; \theta +f_{g})s&=\frac{1}{2}m(0^{2}-v_{o}^{2})\\ -(mg\; sin\; \theta+\mu_{k}mg\; cos\; \theta)s&=-\frac{1}{2}mv^{2}\\ mgs\; sin\; \theta+\mu_{k}mgs\; cos\; \theta&=\frac{1}{2}mv^{2}\\ gh+\mu_{k}gl&=\frac{1}{2}v^{2}\\ v&=\sqrt{2(gh+\mu_{k}gl)}\end{aligned}
Jawaban
E
11. Soal
Sebuah balok bermassa 2 kg mula - mula diam dilepaskan dari puncak bidang lengkung yang berbentuk seperempat lingkaran dengan jejari R. Kemudian balok meluncur pada bidang datar dan berhenti di B yang berjarak 3 m dari titik awal bidang datar A. Jika bidang lengkung tersebut licin sedangkan gaya gesek antara balok dan bidang datar sebesar 8 N maka R adalah? (SPMB 2005)
A. 0,2 m
B. 0,5 m
C. 1,2 m
D. 1,5 m
E. 1,6 m
Pembahasan
Bidang datar kasar AB
\begin{aligned}W&=\Delta E_{k}\\ f_{g}s&=\frac{1}{2}mv_{A}^{2}\\ (8)(3)&=\frac{1}{2}(2)v_{A}^{2}\\ v_{A}^{2}&=24\end{aligned}
Bidang licin CA berlaku hukum kekekalan energi
$E_{pA}+E_{kA}=E_{pC}+E_{kC}$
karena $E_{pA}=0$ dan $E_{kC}=0$ maka:
\begin{aligned} \frac{1}{2}mv_{A}^{2}&=mgh_{c}\\ h_{c}&=\frac{v_{A}^{2}}{2g}\\ R&=\frac{24}{2(10)}\\ R&=1,2\; m \end{aligned}
Jawaban
C
12. Soal
Sebuah beban bermassa m yang diikatkan pada ujung kanan sebuah pegas dengan konstanta pegas k diletakkan pada lantai datar dengan ujung pegas sebelah kiri terikat pada dinding. Beban ditarik ke kanan sampai ke titik A yang berjarak a dari titik setimbang dan kemudian dilepaskan sehingga berisolasi.
Setelah dilepas, beban bergerak ke kiri melewati titik seimbang dan berhenti sesaat pada jarak b di sebelah kiri titik seimbang. Andaikan lantai kasar dengan besar gaya gesek f, energi kinetik di titik setimbang adalah . . . .
A. $\displaystyle \frac{1}{2}ka^{2}$
B. $\displaystyle \frac{1}{2}ka^{2}-fa$
C. $\displaystyle \frac{1}{2}kb^{2}$
D. $\displaystyle \frac{1}{2}ka^{2}+fa$
E. $\displaystyle \frac{1}{2}ka^{2}-fa$
Pembahasan
Permukaan kasar maka terdapat gaya gesek
Energi kinetik di titik seimbang adalah
$\displaystyle E_{kO}=\frac{1}{2}ka^{2}-fa$
Jawaban
B
13. Soal
Sebuah truk bermassa 1000 kg melaju dengan kelajuan kontan 100 km/jam menaiki tanjakan miring dengan kemiringan $tan\; \alpha = 0,1$. Jika gaya gesekan total yang bekerja pada truk adalah 700 N, hitunglah daya minimum yang harus diberikan oleh mesin truk! ($g = 9,81\; m/s^{2}$) (UTUL UGM 2019)
A. 47,1 kW
B. 52,7 kW
C. 62,5 kW
D. 72,8 kW
E. 85,1 kW
Pembahasan
Diketahui
Usaha Energi
m =1000 kg
v = 100 km/jam
$tan\; \theta=0,1$
$\displaystyle sin\; \theta=\frac{1}{\sqrt{101}}$
$v=100\; km/jam$
$\displaystyle v=\frac{100}{3,6}\;m/s$
\begin{aligned} P&=Fv\\ P&= \left(\frac{10000}{\sqrt{101}}+700 \right)\frac{100}{3,6}\\ P&=47222\; watt\\ P&=47\; kWatt\end{aligned}
Jawaban
A
14. Soal
Perhatikan gambar berikut!
Gambar di atas menunjukkan seorang ibu mendorong kereta belanja di atas bidang datar licin dengan gaya F sehingga berjalan dalam selang waktu t. Tabel berikut ini berisi data - data tentang massa (M), gaya dorong (F), dan waktu (t).
Berdasarkan tabel di atas, maka urutan data yang menghasilkan usaha mulai dari terkecil adalah . . . .
A. (1) - (2) - (3) - (4)
B. (1) - (3) - (4) - (2)
C. (2) - (4) - (3) - (1)
D. (3) - (1) - (2) - (4)
E. (4) - (2) - (1) - (3)
Pembahasan
Diketahui
Usaha Energi
\begin{aligned} I&=\Delta p\\ F.t&=m(v_{t}-v_{o})\\ F.t&=m(v-0)\\ v&=\frac{F.t}{m}\end{aligned}
Usaha (W)
\begin{aligned} W&=\Delta E_{k}\\ W&=\frac{1}{2}m(v_{t}^{2}-v_{o}^{2})\\ W&=\frac{1}{2}m(v_{t}^{2}-0^{2})\\ W&=\frac{1}{2}mv^{2}\\ W&=\frac{1}{2}m\left(\frac{Ft}{m}\right)^{2}\\ W&=\frac{1}{2}\frac{F^{2}t^{2}}{m}\end{aligned}
Usaha terkecil maka nilai F dan t kecil dan M besar
maka usaha terkecil adalah tabel no 4
Jawaban E
15. Soal
Sebuah bola pejal dengan massa 4 kg terleak di ujung lemari kemudian didorong mendatar sehingga kecepatannya 2 m/s pada saat lepas dari tepi atas lemari seperti tampak pada gambar di bawah.
Percepatan gravitasi g adalah $10\; m.s^{-2}$, maka energi mekanik partikel pada saat benda berada pada ketinggian 1 m dari tanah sebesar?
A. 40 J
B. 48 J
C. 80 J
D. 88 J
E. 96 J
Pembahasan
Diketahui
Usaha dan Energi
jika diketahui v dan h keadaan licin tidak ada gaya gesek berlaku hukum kekekalan energi
\begin{aligned}E_{m}&= E_{p}+E_{k}\\ E_{m}&= mgh+\frac{1}{2}mv^{2}\\ E_{m}&= (4)(10)(2)+\frac{1}{2}(4)(2)^{2}\\ E_{m}&= 80+8\\ E_{m}&= 88\; joule\end{aligned}
Jawaban D
16. Soal
Sebuah balok bermassa 5 kg bergerak pada sebuah bidang datar licin dengan kecepatan 2 m/s. Kemudian balok tersebut menuruni bidang miring kasar dengan kemiringan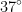 
dan mengalami gaya gesek sebesar 20 N. Setelah sampai dasar bidang miring, balok meluncur pada bidang datar licin pada kecepatan 4 m/s. Jika percepatan gravitasi pada tempat tersebut $10\;m/s^{2}$, kedua bidang datar tersebut mempunyai perbedaan tinggi sebesar . . . .m (UTBK 2021)
A. 0,8
B. 1,2
C. 1,5
D. 1,8
E. 2,0
Pembahasan
Diketahui:
\begin{aligned}E_{m(awal)}&=E_{m(akhir)}\\ E_{p(o)}+E_{k(o)}&=W_{gesek}+E_{k(t)}\\ mgh+\frac{1}{2}mv_{o}^{2}&=f_{gesek}.s +\frac{1}{2}mv_{t}^{2}\\ mgh+\frac{1}{2}mv_{o}^{2}&=f_{gesek}.\frac{h}{sin\; \theta}+\frac{1}{2}mv_{t}^{2}\\ 5.10.h+\frac{1}{2}.5.2^{2}&=20.\frac{h}{0,6}+\frac{1}{2}.5.4^{2}\\ 50h+10&=\frac{100h}{3}+40\\ \frac{50}{3}h&=30\\ h&=\frac{9}{5}\;m\\ h&=1,8\;m\end{aligned}
Jawaban D
17. Soal
Sebuah partikel yang bermassa 0,1 kg dilepas dari titik A tanpa kecepatan awal lalu melewati bidang seperempat lingkaran licin, bidang datar kasar dan berakhir di titik D pada bidang seperempat lingkaran licin seperti pada gambar. Berapakah besarnya sudut $\alpha$?
A. $30^{\circ}$
B. $37^{\circ}$
C. $45^{\circ}$
D. $53^{\circ}$
E. $60^{\circ}$
Pembahasan
Diketahui: Gambar
Ditanya sudut yang dibentuk $\alpha$.....?
Tinjau AB (licin)
$E_{pA}=E_{kB}$
$E_{kB}=mgh$
$E_{kB}=0,1.10.5$
$E_{kB}=5\; joule$
Tinjau BC (kasar)
$E_{kB}=W_{gesek}+E_{kC}$
$E_{kB}=f_{gesek}s+E_{kC}$
$E_{kB}=\mu mgs+E_{kC}$
$5=(0,4)(0,1)(10)(10)+E_{kC}$
$E_{kC}=5-4$
$E_{kC}=1\; joule$
Tinjau BD (licin)
$E_{kC}=E_{pD}$
$E_{kC}=mgh_{D}$
$1=(0,1)(10)h_{D}$
$h_{D}=1\; m$
$cos\; \alpha=\frac {4}{5}$
$\alpha = 37^{\circ}$
Jawaban B
18. Soal
Sebuah rollercoaster memiliki lintasan dengan sebuah loop melingkar vertikal dengan jari - jari R = 4,0 meter. Rollercoster meluncur dari keadaan diam dari suatu ketinggian maksimum h seperti gambar. Anggap bahwa rollercoster meluncur bebas tidak ada gesekan. Tentukan besar h minimum agar rollercoster tetap pada lintasan.
A. 5,0 m
B. 7,5 m
C. 9,0 m
D. 10,0 m
E. 12,5 m
Pembahasan
Diketahui : R = 10 m
Ditanya: h minimum
syarat agar rollercoster tetap pada lintasan dan bisa melakukan satu kali putaran penuh adalah kecepatan minimum dipuncak lintasan sebesar
$v_{minimum}=\sqrt {gR}$
karena permukaan licin, maka berlaku hukum kekekalan energi
posisi 1 : $h_{1}=h$ dan $v_{1}=0$
posisi 2 : $h_{2}=2R$ dan $v_{2}=\sqrt {gR}$
maka:
\begin{aligned} E_{p1}+E_{k1}&=E_{p2}+E_{k2}\\ mgh_{1}+\frac {1}{2}mv_{1}^{2}&=mgh_{2}+\frac {1}{2}mv_{2}^{2}\\ gh+0&=g(2R)+\frac {1}{2}(\sqrt {gR})^{2}\\ gh&=2gR+\frac {1}{2}gR\\ h&=\frac {5}{2}R\\ h&=\frac {5}{2}(4)\\ h&=10\; m \end{aligned}
Jawaban D
19. Soal
Sebuah pistol mainan bekerja dengan menggunakan pegas untuk melontarkan peluru. Jika pistol yang sudah dalam keadaan terkokang yaitu dengan menekan pegas sejauh $x$, diarahkan dengan membuat sudut elevasi $\theta$ terhadap horizontal, peluru yang terlepas dapat mencapai ketinggian $h$. Jika massa peluru adalah $m$ dan percepatan gravitasi adalah $g$, maka konstanta pegas adalah?
A. $\displaystyle k=\frac{2mgh}{x^{2}cos^{2}\theta}$
B. $\displaystyle k=\frac{2mgh}{x^{2}sin^{2}\theta}$
C. $\displaystyle k=\frac{mgh}{x^{2}cos^{2}\theta}$
D. $\displaystyle k=\frac{mgh}{x^{2}sin^{2}\theta}$
E. $\displaystyle k=\frac{mgh}{x^{2}tan^{2}\theta}$
20. Soal
Benda A yang memiliki massa 0,5 kg dan mula - mula diam meluncur 3m pada papan licin yang membentuk sudut $30^{\circ}$ dengan bidang datar. Kemudian benda A menumbuk pegas P yang salah satu ujungnya tertanacap kuat pada ujung papan. JIka konstanta pegas 900 N/m, maka pemendekan maksimum pegas adalah?
A. 4,9 cm
B. 8,7 cm
C. 10,6 cm
D. 12,9 cm
E. 18,7 cm
