Pembahasan Soal Pegas

Solusi Soal Pegas

1. Soal

Sebuah balok bermassa 144 gram di atas lantai datar yang licin dihubungkan dengan tiga buah pegas dengan susunan seperti dilukiskan dalam gambar di atas. Konstanta - konstanta pegasnya masing - masing adalah $k_{1}=20\;N/m,\; k_{2}=20\;N/m$ dan $k_{3}=60\;N/m$. Jika balok disimpangkan dari titik seimbangnya dengan simpangan kecil, maka periode getaran harmonis yang dihasilkan mendekati? (SIMAK UI 2009)

A. $ 12\pi$ detik
B. $ 6\pi$ detik

C. $ \pi$ detik

D. $ 1,2\pi$ detik

E. $ 0,12\pi$ detik

Pembahasan

Pegas 2 dan 3 disusun seri maka nilai 

\begin{aligned} k_{2,3}&=\frac{k_{2}\times k_{3}}{k_{2}+k_{3}}\\ k_{2,3}&=\frac{60\times 30}{60+30}\\ k_{2,3}&=20\;N/m\end{aligned}
Nilai konstanta pegas total

\begin{aligned}k_{total}&=k_{1}+k_{2,3}\\ k_{total}&=20+20\\ k_{total}&=40\;N/m\end{aligned}
Periode getaran harmonis

\begin{aligned}T&=2\pi \sqrt{\frac{m}{k}}\\ T&=2\pi \sqrt{\frac{144\times 10^{-3}}{40}}\\ T&=0,12\pi \;detik\end{aligned}
Jawaban E
2. Soal

Sebuah mobil angkot memiliki massa 1.350 kg menggunakan 4 buah pegas identik untuk peredam kejutnya. Dengan konstanta pegas 13.500 N/m, ketika melewati sebuah lubang, mobil itu berisolasi dengan frekuensi $\frac{3}{\pi}$ Hz. Jika diandaikan massa rata - rata orang dewasa adalah 75 kg, jumlah penumpang pada mobil tersebut adalah? (SIMAK UI 2016)

A. 1 orang
B. 3 orang
C. 5 orang
D. 7 orang
E. 9 orang
Pembahasan

Diketahui

$k_{total}=4\times k=4\times 13500=54000\; N/m$

$m_{mobil}=1350\;kg$
$m_{orang}=75\;kg$

maka:

\begin{aligned} f&=\frac{1}{2\pi}\sqrt{\frac{k}{m}}\\ f&=\frac{1}{2\pi}\sqrt{\frac{k_{mobil}}{m_{mobil}+(n.m_{orang})}}\\ \frac{3}{\pi}&=\frac{1}{2\pi}\sqrt{\frac{54000}{1350+75n}}\\ 1500&=1350+75n\\ 75n&=150\\ n&=2\;orang\end{aligned}

jumlah orang dalam mobil adalah 2 yaitu sopir dan 1 penumpang
Jawaban A
3. Soal

Suatu pegas dengan konstanta pegas k diregangkan sebesar x. Seandainya separuh usaha yang digunakan untuk meregangkan pegas kedua, pegas kedua ternyata teregang sebesar x/4. Maka konstanta pegas kdua adalah . . . k (UM UGM 2016)

A. 2
B. 4
C. 6
D. 8
E. 32
Pembahasan

Diketahui
$k_{1}=k$

$x_{1}=x$

$x_{2}=x/4$

$W_{1}=W$
$W_{2}=W/2$
$k_{2} = . . . .  ?$
Rumus usaha pegas $W=\frac{1}{2}kx^{2}$, maka:

\begin{aligned} \frac{W_{1}}{W_{2}}&=\frac{k_{1}x_{1}^{2}}{k_{2}x_{2}^{2}}\\ \frac{W}{W/2}&=\frac{kx^{2}}{k_{2}(x/4)^{2}}\\ 2&=\frac{16k}{k_{2}}\\ k_{2}&=8k\end{aligned}
Jawaban D

4. Soal

Jika periode bandul sederhana bergantung pada panjang bandul L dan percepatan gravitasi g dengan dimensi $\frac{L}{T^{2}}$, manakah ungkapan periode bandul sederhana yang benar dengan k adalah sebuah tetapan ? (UM UGM 2017)

A. $T=k\sqrt{L}{g}$
B. $T=k\sqrt{Lg}$
C. $T=k\sqrt{g}{L}$
D. $T=k\sqrt{Lg}$
E. $T=kLg$
Pembahasan

Periode bandul

$T=2\pi \sqrt{\frac{L}{g}}$
k = konstanta
$T=k\sqrt{\frac{L}{g}}$
Jawaban A

5. Soal

Sebuah pegas dengan konstanta pegas sebesar A, jika saat ditarik mengalami perubahan panjang sebesar B, maka energi potensial elastis pegas adalah? (SIMAK UI 2009)

A. $A.B$
B. $A.B^{2}$
C. $A^{2}B$
D. $\frac{1}{2}A^{2}B$
E. $\frac{1}{2}AB^{2}$
Pembahasan

$k=A$
$x=B$

$E_{p}= . . . . ?$

maka

$E_{p}=\frac{1}{2}kx^{2}$

$E_{p}=\frac{1}{2}AB^{2}$
Jawaban E

6. Soal

Sebuah mobil bermassa M secara sederhana dapat dianggap sebagai benda di atas sebuah pegas dengan tetapan pegas k. Untuk mobil saja pegas mempunyai frekuensi osilasi alamiah $f_{1}$. Jika beberapa penumpang dengan massa m berada dalam mobil, frekuensi osilasi menjadi $f_{2}$. Nilai $f_{1}/f_{2}$ dengan mengabaikan redaman yang muncul dalam sistem besarnya?

A. $\displaystyle \sqrt{\frac{M+m}{M}}$
B. $\displaystyle \frac{M+m}{M}$
C. $\displaystyle \sqrt{\frac{M}{M+m}}$
D. $\displaystyle \frac{M}{M+m}$
E. $\displaystyle \left(\frac{M+m}{M}\right)^{2}$
Pembahasan
Diketahui

$m_{1}=M$
$m_{2}=M+m$

$f_{1}/f_{2}= . . . . ?$

maka:

\begin{aligned}f&=\frac{1}{2\pi}\sqrt{\frac{k}{m}}\\ \frac{f_{1}}{f_{2}}&=\sqrt{\frac{m_{2}}{m_{1}}}\\ \frac{f_{1}}{f_{2}}&=\sqrt{\frac{M+m}{M}}\end{aligned}
Jawaban A
7. Soal

 Sebuah pegas dengan tetapan $k_{1}$  berisolasi dengan frekuensi $\omega$  saat diberi beban dengan massa $M$. Agar pegas kedua dengan tetapan pegas $k_{2}=2k_{1}$ berosilasi dengan  $\omega =\frac{\omega}{2}$, maka beban yang harus diberikan adalah? (SBMPTN 2017)
A. 2 M
B. 4 M
C. 6 M
D. 8 M
E. 10 M
Pembahasan
Diketahui
$k_{1}$
$m_{1}=M$
$k_{2}=2k_{1}$
$\omega =\frac{\omega}{2}$

$m_{2}=  . . . .?$

$f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$

maka:

\begin{aligned}\frac{f_{1}}{f_{2}}&=\sqrt{\frac{k_{1}m_{2}}{k_{2}m_{1}}}\\ \frac{\omega}{\omega/2}&=\sqrt{\frac{k.m_{2}}{2k.M}}\\ 2&=\sqrt{\frac{m_{2}}{2M}}\\ m_{2}&=8M\end{aligned}

Jawaban D

8. Soal
Sebuah bola dengan massa 20 gram digantung pada sepotong per (pegas). Kemudian, bola ditarik ke bawah dari kedudukan seimbang lalu dilepaskan, ternyata terjadi getaran tunggal dengan frekuensi 32 Hz. Jika bola tersebut diganti dengan massa bola 80 gram maka frekuensi yang akan terjadi adalah . . .  Hz (UMPTN 1991)
A. 64
B. 32
C. 16
D. 8
E. 4
Pembahasan
Diketahui

$m_{1}=20\; gram$

$m_{2}=80\; gram$

$f_{1}=32\;Hz$
$f_{2}= . . . . .?$

maka:

$f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$

maka:

\begin{aligned} \frac{f_{1}}{f_{2}}&=\sqrt{\frac{m_{2}}{m_{1}}}\\ \frac{32}{f_{2}}&=\sqrt{\frac{80}{20}}\\ \frac{32}{f_{2}}&=\sqrt{4}\\ \frac{32}{f_{2}}&=2\\ f_{2}&=16\;Hz\end{aligned}
Jawaban C
9. Soal
Besar usaha yang dikeluarkan untuk memanjangkan pegas sejauh 2 cm adalah 0,5 joule. Untuk memanjangkan pegas itu sejauh 4 cm akan diperlukan gaya (dalam N) sebesar? (UM UGM 2006)
A. 1
B. 10
C. 100
D. 1000
E. 10000
Pembahasan
Diketahui
$x = 2\; cm=2\times 10^{-2}m$
$W = 0,5\; joule$

Maka

\begin{aligned} W&=\frac{1}{2}kx^{2}\\ 0,5&=\frac{1}{2}k(2\times 10^{2})^{2}\\ k&=2500\;N/m\end{aligned}
 jika $x_{2}=4\;cm=4\times 10^{-2}m$ 

\begin{aligned}F&=kx\\ F&=2500(4\times 10^{-2})\\ F&=100\;N\end{aligned}

Jawaban C
10. Soal

Dua buah pegas dengan konstanta yang sama k, dipasang pada sebuah benda bermassa m seperti tampak pada gambar. Mula - mula kedua pegas memiliki panjang tak teregang sebesar L. Benda kemudian digeser sejauh x ke titik A pada arah tegak lurus susunan pegas (lihat gambar). Usaha yang dilakukan kedua pegas terhadap benda ketika benda bergerak dari posisi A ke posisi mula - mula adalah (UM UGM 2009)
A. $2k(\sqrt{x^{2}+L^{2}}-L)^{2}$
B. $k(\sqrt{x^{2}+L^{2}}+L)^{2}/2$
C. $k(x^{2}-L^{2})$
D. $kx^{2}/2$

E. $k(\sqrt{x^{2}+L^{2}}-L)^{2}$

Pembahasan

Diketahui

$k_{total}=2k$
$L_{t}=\sqrt{L^{2}+x^{2}}$
$\Delta x=\Delta L=L_{t}-L=\sqrt{L^{2}+x^{2}}-L$
maka:

\begin{aligned}W&=\frac{1}{2}k_{total}\Delta x^{2}\\ W&=\frac{1}{2}2k(\sqrt{L^{2}+x^{2}}-L)^{2}\\W&=k(\sqrt{L^{2}+x^{2}}-L)^{2}\end{aligned}
Jawaban E
11. Soal

Dua buah pegas identik, jika terpasang paralel dibutuhkan usaha sebesar W untuk menarik pegas supaya bertambah panjang sebesar x. Kemudian keduanya dipasang secara seri. Berapakah usaha yang dibutuhkan pegas yang tersusun seri tersebut aga kedua pegas tertekan sebesar x? (UTUL UGM 2019)

A. W/4

B. W/2

C. W

D. 2W

E. 4W

Pembahasan
Diketahui
Elastisitas - Pegas
$k_{1}=2k$  $x_{1}=x$   $W_{1}=W$2
$k_{2}=\frac{k}{2}$  $x_{2}=x$    $W_{2}= . . . . ?$
maka :

\begin{aligned}\frac{W_{1}=\frac{1}{2}k_{1}x_{1}^{2}}{W_{2}=\frac{1}{2}k_{2}x_{2}^{2}}\\ \frac{W_{1}=k_{1}x_{1}^{2}}{W_{2}=k_{2}x_{2}^{2}}\\ \frac{W=2k.x^{2}}{W_{2}=\frac{k}{2}x^{2}}\\ \frac{W}{W_{2}}&=\frac{4}{1}\\ W_{2}&=\frac{1}{4}W\end{aligned} 

Jawaban A
12. Soal

Perhatikan empat susunan rangkaian pegas identik berikut!

Konstanta tiap pegas adalah k (N/m), maka urutan konstanta pengganti susunan pegas dari nilai yang besar ke kecil adalah?

A. (4), (3), (2), dan (1)

B. (3), (2), (1), dan (4)

C. (2), (1), (4), dan (3)

D. (2), (3), (4), dan (1)

E. (1), (4), (3), dan (2)

Pembahasan

Diketahui

Pegas

Susunan pegas

Seri ==> Se-per

Paralel ==> Jumlah

$k_{1}=2,5k$
$k_{2}=\frac{3}{5}k$
$k_{3}=\frac{3}{4}k$
$k_{4}=k$
Urutan konstanta pengganti pegas yang besar ke kecil
(1) - (4) - (3) - (2)
Jawaban E

13. Soal

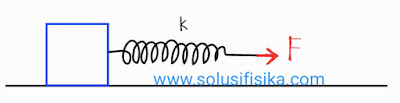
Sebuah pegas ringan memiliki tetapan pegas 500 N/m. Salah satu ujung pegas itu diikat pada balok yang terletak di lantai yang cukup licin, sedangkan ujung yang lain ditarik (lihat gambar) sehingga balok mengalami percepatan 20 $m/s^{2}$. Jika massa balok 1 kg, brapakah energi potensial pegas?

A. 0,4 joule
B. 0,6 joule
C. 0,8 joule
D. 1,0 joule
E. 1,2 joule
Pembahasan
Diketahui
$k=500\;N/m$
$m= 1\;kg$
$a= 20\;m/s^{2}$
maka
\begin{aligned}F&=kx\\ ma&=kx\\ 1\times 20&=500x\\ x&=\frac{1}{25}m\end{aligned}
Maka Energi Potensial
\begin{aligned} E_{p}&=\frac{1}{2}kx^{2}\\ E_{p}&=\frac{1}{2}.500.\left(\frac{1}{25}\right)^{2}\\ E_{p}&=250\left(\frac{1}{625}\right)\\ E_{p}&=0,4\;joule \end{aligned}
Jawaban A

14. Soal

Sebuah pegas ringan memiliki tetapan pegas 500 N/m. Salah satu ujung pegas itu diikat pada balok yang terletak di lantai yang cukup licin, sedangkan ujung yang lain ditarik $($lihat gambar$)$ dengan gaya yang tetap, sehingga balok mengalami percepatan $5\; m/s^{2}$ dan pegas bertambah panjang 1 cm. Jika di atas balok itu diletakkan sebuah balok lain yang bermassa sama sehingga perceptannya menjadi $2,5\; m/s^{2}$, berapakah pertambahan panjang pegas sekarang?

A. 1,0 cm
B. 2,0 cm
C. 2,4 cm
D. 2,8 cm
E. 3,2 cm
Pembahasan
Diketahui
pegas $k =\;500\;N/m$
$a_{1}=5\; m/s^{2}$ dan $x_{1}=1\;cm$
$m_{1}=m$
$a_{1}=5\; m/s^{2}$ dan $x_{2}=. . . . ?$
$m_{2}=2m$
Benda terhubung pegas ditarik dengan gaya F
Rumus
\begin{aligned} F&=kx\\ ma&=kx \end{aligned}
\begin{aligned} \frac{m_{1}.a_{1}}{m_{2}.a_{2}}&=\frac{k.x_{1}}{k.x_{2}}\\  \frac{m_{1}.a_{1}}{m_{2}.a_{2}}&=\frac{x_{1}}{x_{2}}\\  \frac{m.5}{2m. 2,5}&=\frac{x}{x_{2}}\\ x_{2}&=\;1\; cm \end{aligned}
Jawaban A

15. Soal

Suatu pegas dengan konstanta pegas k diregangkan sebesar x. Seandainya separuh usaha yang digunakan untuk meregangkan pegas tadi dipakai untuk meregangkan pegas kedua, pegas kedua ternyata teregang sebesar $x/4$. Maka konstanta pegas kedua adalah . . . k (UM UGM 2016)
A. 2
B. 4
C. 6
D. 8
E. 32
Pembahasan

Diketahui
Keadaan Pertama(1)
$k_{1}=k$
$x_{1}=x$
$W_{1}=W$
Keadaan Kedua (2)
$k_{2}= . . . .?$
$x_{2}=x/4 $
$W_{2}=\frac{1}{2}W$
Maka:
\begin{aligned} \frac{W_{1}}{W_{2}}&=\frac{\frac{1}{2}k_{1}x_{1}^{2}}{\frac{1}{2}k_{2}x_{2}^{2}}\\  \frac{W}{\frac{1}{2}W}&=\frac{k.x^{2}}{k_{2}.(x/4)^{2}}\\ 2&=\frac{k.x^{2}}{k_{2}.x^{2}/16}\\ 2&=\frac{16k}{k_{2}}\\ k_{2}&=8k \end{aligned}

Jawaban D