Pembahasan Soal Gelombang Mekanik dan Stasioner

Solusi Soal Gelombang Mekanik dan Stasioner

1. Soal

Sebuah tali digetarkan dengan frekuensi 5 Hz menghasilkan gelombang beramplitudo 12 cm dan kelajuan gelombang 20 m/s. Dari pernyataan berikut yang sesuai dengan gelombang yang dihasilkan oleh getaran tali adalah...(SNMPTN 2007)

(1) Frekuensi angular gelombang 31,4 rad/s

(2) Panjang gelombang 6 m

(3) Persamaan gelombang $y=0,12\, sin\, 2\pi (0,25x-5t)m$

(4) Angka gelombang 1,57 /m

Pembahasan

(1) $\omega =2\pi f=2.3,14.5=31,4\, rad/s$

(2) $\lambda =\frac{v}{f}=\frac{20}{5}=4\, m$

(3) $y=A\, sin\, \left ( \omega t-kx \right )$

$y=0,12\, sin\, \left ( 10\pi t-\frac{1}{2}\pi x \right )$

$y=0,12\, sin\, 2\pi \left ( 5 t-\frac{1}{4} x \right )$

(4) $k=\frac{2\pi }{\lambda }=\frac{2\pi }{4 }=1,57$

Jawaban D

2. Soal

Persamaan gelombang tranversal yang merambat sepanjang tali yang sangat panjang dapat dinyatakan dengan persamaan $y=6\, sin\, \left ( 0,02\pi x+4\pi t\right )$ dengan y dan x dalam cm serta t dalam sekon. Ini berarti bahwa ..... (SNMPTN 2008)

(1) Amplitudo gelombangnya adalah 6 cm

(2) Panjang gelombangnya 1 m

(3) Frekuensi gelombangnya adalah 2 Hz

(4) Penjalaran gelombangnya adalah ke arah sumbu x positif

Pembahasan

$y=6\, sin\, \left ( 0,02\pi x+4\pi t\right )$

$y=A\, sin\, \left ( kx+\omega t\right )$

(1) A = 6 cm

(2) Panjang gelombang

$k=\frac{2\pi }{\lambda }$

$0,02\pi =\frac{2\pi }{\lambda }$

$\lambda=\frac{2\pi }{0,02\pi }=100\, cm=1\, m$

(3) Frekuensi

$\omega =2\pi f$

$4\pi =2\pi f$

$f=2\, Hz$

(4) arah rambat gelombang ke sumbu x negatif

Jawaban A

3. Soal

Gelombang berjalan memiliki persamaan:

$y(x,t)=0,008\, sin\, (10\pi x-8\pi t)$ dimana y dan x dalam meter dan t dalam detik. Pernyataan yang BENAR adalah . . . . (SIMAK UI 2012)
1) Kecepatan gelombang adalah 0,8 m/detik
2) Frekuensi gelombang 4 Hz
3) Panjang gelombang adalah 0,2 m
4) Simpangan pada titik 10 m dan waktu 100 detik adalah 0,004 m
Pembahasan
Diketahui
$y(x,t)=0,008\, sin\, (10\pi x-8\pi t)$
$y=A\, sin\, \left ( kx-\omega t\right )$
maka:
A = 0,008 m
1. Cepat rambat gelombang (v)
   $v= \frac{keof\, \, t}{koef\, \, x}$
   $v= \frac{8\pi }{10\pi }=0,8\, \, m/s$
2. Frekuensi ( f )
   $\omega =2\pi f$
$8\pi = 2\pi f$
   $f=4\, \, Hz$
3. Panjang gelombang
   $k=\frac{2\pi }{\lambda }$
$10\pi =\frac{2\pi }{\lambda }$
   $\lambda =0,2\, m$
4. Simpangan (y)
t = 100 s dan x = 10 m
$y=0,08(100\pi -800\pi )$
$y=0,08(-700\pi )$
$y=0\, \, m$
Jawaban A
4. Soal

Suatu gelombang sinusidal bergerak dalam arah x - positif, mempunyai amplitudo 15,0 cm panjang gelombang 40,0 cm dan frekuensi 8,0 Hz. Jika posisi vertikal dari elemen medium pada t = 0 dan x = 0 adalah 15,0 cm, maka bentuk umum fungsi gelombangnya adalah? (x dalam cm dan t dalam sekon) (SBMPTN 2014)

A. $y=(15,0\, cm)sin (0,157x+50,3t-\frac{\pi }{2})$
B. $y=(15,0\, cm)sin (0,157x-50,3t+\frac{\pi }{2})$
C. $y=(15,0\, cm)sin (0,157x+50,3t+\frac{\pi }{2})$
D. $y=(15,0\, cm)cos (0,157x-50,3t)$
E. $y=(15,0\, cm)cos (0,157x+50,3t)$
Pembahasan
Diketahui
A = 15 cm
$\lambda =$ 40 cm
$f=$ 8 Hz
pada saat t = 0 s dan x = 0 m nilai y = 15 cm maka sudut fase awal ( $\theta _{o}=90^\circ$ )
Nilai kecepatan sudut
$\omega =2\pi f$
$\omega=2\pi 8=16\pi \, \, rad/s$
Nilai bilangan gelombang
$k=\frac{2\pi }{\lambda }$
$k=\frac{2\pi }{40}=0,05\pi /m$
gelombang merambat ke sumbu x(+)
maka persamaan gelombang memenuhi
$y=Asin(\omega t-kx+\theta _{o})$
$y=15sin(16\pi t-0,05\pi x+90^{\circ })$
inget sifat trigonometri   $y=sin(\alpha +90)=cos\, \alpha$
$y=15cos(16\pi t-0,05\pi x)$
inget juga $y=cos\, \alpha = cos\, (-\alpha)$
$y=15cos(0,05\pi x-16\pi t)$
$y=15cos(0,157 x-50,3 t)$
Jawaban D
5. Soal
Dua benda masing - masing menjalani gerak harmonis sederhana dengan persamaan masing - masing
$y_{1}=8\sin 100t, y_{2}=6\sin \left ( 10t-\frac{\pi }{2} \right )$
dengan x dan y dalam cm sedangkan t dalam setik, besar amplitudo superposisi dari kedua getaran adalah? (SPMB 2007)
A. 14 cm
B. 10 cm
C. 8 cm
D. 6 cm
E. 2 cm
Pembahasan
Terdapat 2 getaran yang memiliki beda fase π/2 maka kedua getaran saling tegak lurus.
$A_{total}=\sqrt{A_{1}^{2}+A_{2}^{2}}=\sqrt{8^{2}+6^{2}}=10$
Jawaban B
6. Soal
Gelombang bunyi dari sumber   $S_{1}$ dan $S_{2}$ menimbulkan simpangan di tiitk P sbb:
$y_{1}=A\, cos\left ( kr_{1}-\omega t \right )$
$y_{2}=A\, cos\left ( kr_{2}-\omega t \right )$
dengan laju bunyi 350 m/s, frekuensi f = 700 Hz. Maka : (UMPTN 2001)
1) panjang gelombang bunyi tersebut 0,5 m
2) interferensi konstruktif terjadi bila   $r_{2}-r_{1}=1,5\, m$
3) intrferensi minimum di P terjadi bila $r_{2}-r_{1}=1,25\, m$
4) intensitas maksimum di $P=2A^{2}$
Pembahasan
Diketahui
v = 350 m/s
f = 700 Hz
1) Panjang gelombang
   $\lambda =\frac{v}{f}=\frac{350}{700}=0,5 \, \, m$
2) Interferensi konstruktif
pola: 1 $\lambda$ , 2 $\lambda$ , 3 $\lambda$ dst
maka 1,5 m adalah interferensi kontruktif
3) Interferensi minimum
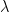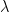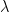pola: 0,5 $\lambda$ , 1,5 $\lambda$ , 2,5 $\lambda$ dst
maka 1,25 m adalah interfernsi minium
4)Intensitas maksimum
   $I=\frac{P}{A}=\frac{E}{4\pi r^{2}t}=\frac{\frac{1}{2}kA^{2}}{4\pi r^{2}t}$

$I\sim A_{s}^{2}\sim (2A)^{2}\sim 4A^{2}$

Jawaban A
7. Soal
Sebuah gelombang pada tali menjalar dengan persamaan : $y=0,12sin\,(\frac{\pi }{8}x+ 4\pi t)$ , x dalam meter dan t dalam detik. Persamaan tersebut mempunyai pengertian bahwa . . .

(1) persamaan kecepatan gelombangnya

   $v=\frac{dy}{dt}=(0,12)(4\pi )cos\,(\frac{\pi }{8}x+ 4\pi t)$
(2) kecepatan maksimum gelombang
   $v=0,48\pi \, m/s$
(3) persamaan percepatan gelombang
   $a=(-0,12)(4\pi )^{2}sin\,(\frac{\pi }{8}x+ 4\pi t)$
(4) percepatan maksimum gelombang
   $a=1,92\pi^{2} \, m/s^{2}$
Pembahasan
Diketahui
simpangan ke kecepatan diferensialkan
kecepatan ke percepatan diferensialkan
$y=0,12sin\,(\frac{\pi }{8}x+ 4\pi t)$
$v=\frac{dy}{dt}=(0,12)(4\pi )cos\,(\frac{\pi }{8}x+ 4\pi t)$
$a=(-0,12)(4\pi )^{2}sin\,(\frac{\pi }{8}x+ 4\pi t)$
v maksimum cos sudut bernilai 1
$v=0,48\pi \, m/s$
a maksimum sin sudut bernilai 1
$a=1,92\pi^{2} \, m/s^{2}$
Jawaban E
8. Soal

Gambar di atas merupakan gelombang yang merambat pada seutas tali. Gelombang yang tampak pada gambar terjadi setelah sumber gelombang bergetar selama 6 detik. Pernyataan yang BENAR terkait dengan gelombang tersebut adalah . . . .

(1) Frekuensi gelombang adalah 2 Hz
(2) Cepat rambat gelombang adalah 0,3 m/s
(3) Persamaan simpangan adalah
$y=0,6sin\, 2\pi (2t-\frac{x}{0,6})$
(4) Simpangan di titik yang berjarak 90 cm adalah 0
Pembahasan
Diketahui
n = 3
x = 1,8 m
A = 0,6 cm
t = 6 sekon
1) Frekuensi (f)
   $f=\frac{n}{t}=\frac{3}{6}=0,5\, Hz$
2) Cepat rambat gelombang
   $v=\frac{x}{t}=\frac{1,8}{6}=0,3\, \, m/s$
3) Persamaan
   $\omega =2\pi f=2\pi (0,5)=\pi \, rad/s$
   $\lambda =\frac{x}{n}=\frac{1,8}{3}=0,6\, m$
   $k=\frac{2\pi }{\lambda }=\frac{2\pi }{0,6}=\frac{10\pi }{3}\, \, /m$
maka :
   $y=A\, sin\, \left ( kx-\omega t\right )$
   $y=6\, sin\, (\pi t-\frac{10\pi }{3}x)$
4) jika x = 90 cm = 0,9 m dan t = 6 sekon, maka:
   $y=6\, sin\, (\pi t-\frac{10\pi }{3}x)$
   $y=6\, sin\, (\pi (6))-\frac{10\pi }{3}(0.9))$

$y=6\, sin\, (3\pi )$

$y=0\, cm$

Jawaban C (2 dan 4)
9. Soal
Gelombang berjalan pada tali dapat dinyatakan dalam persamaan berikut:
$Y=2sin(20\pi t-10\pi x)$ dengan y dalam cm, t dalam detik dan x dalam meter, pernyataan berikut yang betul adalah? (UM UNDIP 2008)
(1) frekuensi gelombang tersebut 10 Hz
(2) panjang gelombangnya 20 cm
(3) cepat rambat gelombang tersebut adalah 2 m/s
(4) dua titik yang berjarak 50 cm adalah sefase
Pembahasan
Diketahui persamaan gelombang berjalan
$Y=2sin(20\pi t-10\pi x)$
$y=A\, sin\, \left ( \omega t-kx \right )$
A = 2 cm
$\omega =20\pi \, rad/s$
$k=10\pi \, /m$
1) frekuensi gelombang
   $f=\frac{\omega }{2\pi }=\frac{20\pi }{2\pi }=10\, \, Hz$
2) panjang gelombang
   $\lambda =\frac{2\pi }{k}=\frac{2\pi }{10\pi }=0,2\, \, m$
3) cepat rambat gelombang
   $v=\frac{koef.\, t}{koef.\, x}=\frac{20\pi }{10\pi }=2 \, m/s$
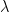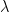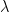4) dua titik yang sefase jika berjarak 1 $\lambda$ , 2 $\lambda$ dst
1 $\lambda$ = 0,2 m = 20 cm
2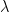 $\lambda$ = 0,4 m = 40 cm
Jawaban A (1,2,3)
10. Soal
Suatu gelombang stasioner memenuhi $y=10sin(0,2\pi x)cos(80\pi t) cm$ , dengan x dalam centimeter dan t dalam sekon. Pernyataan di bawah ini yang benar adalah? (SNMPTN 2012)

1) besar amplitudo tetap 10 cm
2) pada x = 5 cm dari ujung tetap terjadi amplitudo minimum
3) panjang gelombang adalah 1 cm
4) frekuensi gelombang adalah 40 Hz
Pembahasan

Diketahui persamaan gelombang stasioner ujung terikat
$y=10sin(0,2\pi x)cos(80\pi t) cm$
$y=2Asin(kx)cos(\omega t)$
1) Amplitudo
$2A=10\;cm$
$A=5\; cm$
2) Pada jarak x = 5 cm
$A_{s}=10sin(0,2\pi x)$
$A_{s}=10sin(0,2\pi (5))$
$A_{s}=10sin(\pi)$
$A_{s}=0\; cm$
3) panjang gelombang
\begin{aligned} k&=\frac{2\pi}{\lambda}\\ \lambda &=\frac{2\pi}{k}\\ \lambda &=\frac{2\pi}{0,2\pi}\\ \lambda &=10\; m \end{aligned}
4) frekuensi gelombang (f)
\begin{aligned} \omega &=80\pi \; rad/s\\ 2\pi f &=80\pi \\ f&=40\; Hz \end{aligned}
Jawaban C (2 dan 4)

11. Soal
Suatu gelombang stasioner mempunyai $y=\;0,2cos(5\pi x)sin(10\pi t)$ (y dan x dalam meter dan t dalam sekon). Pernyataan yang BENAR adalah

(1) jarak antara perut dan simpul yang berurutan adalah 0,1 m
(2) frekuensi gelombangnya adalah 5 Hz
(3) panjang gelombangnya 0,4 m
(4) kecepatan gelombang 1 m/s
Pembahasan

Diketahui persamaan gelombang stasioner ujung bebas

$y=\;0,2cos(5\pi x)sin(10\pi t)$

$y=2Acos(kx)sin(\omega t)$

maka :

$2A= 0,2\; m$

$A= 0,1\;n$

$k=\;5\pi\; /m$

$\omega=\; 10\pi\; rad/s$

maka:

1) jarak perut ke simpul adalah

$P-S=\frac{1}{4}\lambda=\frac{1}{4}(0,4)=0,1\; m$

2) frekuensi gelombang (f)

\begin{aligned} \omega &=10\pi \; rad/s\\ 2\pi f &=10\pi \\ f&=5\; Hz \end{aligned}

3) panjang gelombang

\begin{aligned} k&=\frac{2\pi}{\lambda}\\ \lambda &=\frac{2\pi}{k}\\ \lambda &=\frac{2\pi}{5\pi}\\ \lambda &=0,4\; m \end{aligned}

4) kecepatan rambat gelombang (v)

$v=\frac{koef. t}{koef. x}=\frac{10\pi}{5\pi}=2\; m/s$

Jawaban A(1,2 dan 3)

12. Soal

Sebuah gelombang tranversal menjalar dengan laju v pada sebuah tali yang memiliki tegangan tali T. Berapakah tegangan tali yang diperlukan agar gelombang menjalar dengan laju $\frac{2v}{3}$ ? (UTUL UGM 2019)

A. $\frac{9}{4}T$

B. $\frac{5}{4}T$

C. $\frac{11}{9}T$

D. $\frac{7}{9}T$

E. $\frac{4}{9}T$

Pembahasan
Diketahui
Gelombang
$F_{1}=T$
$F_{2}=....?$
$v_{1}=v$
$v_{2}=\frac{2v}{3}$
v = kelajuan gelombang tranversal pada tali
$v=\sqrt{\frac{FL}{m}}$
$v\sim \sqrt{T}$
maka:
$\frac{v_{1}}{v_{2}}=\sqrt{\frac{F_{1}}{F_{2}}}$
$\frac{v}{\frac{2}{3}v}=\sqrt{\frac{T}{F_{2}}}$
$\frac{9}{4}=\frac{T}{F_{2}}$
$F_{2}=\frac{4}{9}T$
Jawaban E
13. Soal

Dua buah gelombang masing - masing merambat dengan persamaan simpangan

$y_{1}=0,01\, cos\, 2\pi \left ( \frac{10}{\pi }x-50t \right )$

$y_{2}=0,01\, cos\, \left (20x+100\pi t \right )$

dengan y dan x dalam meter serta t dalam sekon. Apabila superposisi kedua gelombang tersebut menghasilkan gelombang stasioner, simpangan yang ditempuh pada waktu = 0,02 s dan pada $x=\frac{\pi }{60}$ m adalah ..... (SIMAK UI 2014)

A. 0,05 m

B. 0,04 m

C. 0,03 m

D. 0,02 m

E. 0,01 m

Pembahasan

Diketahui
Gelombang pertama

$y_{1}=0,01\, cos\, 2\pi \left ( \frac{10}{\pi }x-50t \right )$
$y_{1}=0,01\, cos\, 2\pi \left ( \frac{10}{\pi }\left ( \frac{\pi }{60} \right )-50(0,02) \right )$
$y_{1}=0,01\, cos\, 2\pi \left ( \frac{1}{6}-1 \right )$
$y_{1}=0,01\, cos\, 2\pi \left ( -\frac{5}{6} \right )$
$y_{1}=0,01\, cos\,\left ( -\frac{5\pi }{3} \right )$
$y_{1}=0,01\, \left ( \frac{1}{2} \right )$
$y_{1}=0,005\, m$

Gelombang kedua
$y_{2}=0,01\, cos\, \left (20x+100\pi t \right )$

$y_{2}=0,01\, cos\left ( 20\left ( \frac{\pi }{60} \right ) +100\pi (0,02)\right )$
$y_{2}=0,01\, cos\left ( \frac{\pi }{3} +2\pi \right )$
$y_{2}=0,01(\frac{1}{2} )$
$y_{2}=0,005\, m$
Superposisi kedua gelombang
$y=y_{1}+y_{2}=0,005+0,005=0,01\, m$
Jawaban E
14. Soal

Seorang anak menjatuhkan sebuah kayu di permukaan air sehingga pada permukaan air terbentuk gelombang. Jika mengganggap persamaan simpangan gelombang yang dihasilkan $y=6sin(0,2\pi t+0,5\pi x)$ dimana y dan x dalam cm dan t dalam sekon, dapat disimpulkan:

(1) Amplitudo gelombang 6 cm

(2) Frekuensi gelombang 0,4 Hz

(3) Panjang gelombang 4 cm

(4) Cepat rambat gelombang 1,6 $cm.s^{-1}$
Kesimpulan yang benar
A. (1) dan (2)
B. (1) dan (3)
C. (2) dan (3)
D. (2) dan (4)
E. (3) dan (4)

Pembahasan

Diketahui

Gelombang Mekanik

$y=6sin(0,2\pi t+0,5\pi x)$

$y=A\, sin\, (\omega t+kx)$
a. Ampitudo
   $A=6\, cm$
b. Kecepatan Sudut
   $\omega =0,2\pi$
$2\pi f=0,2\pi$
$f=0,1\, Hz$
c. Panjang Gelombang
   $k=0,5\pi \, /cm$
$\frac{2\pi }{\lambda }=0,5\pi \, /cm$
   $\lambda =\frac{2}{0,5}$
   $\lambda =4\, cm$
d. Cepat rambat
   $v=\frac{koef\, t}{koef\, x}$
   $v=\frac{0,2\pi }{0,5\pi }$
   $v=0,4\, \, cm/s$
Jawaban B

15. Soal

Perhatikan gambar gelombang berikut ini!

Dari gambar tersebut titik - titik yang mempunyai fase 1,5 adalah?
A. P dengan V
B. P dengan U
C. Q dengan U
D. Q dengan T
E. R dengan S
Pembahasan

Diketahui

Gelombang Mekanik

Fase adalah posisi partikel pada gelombang

fase mirip jumlah gelombang

dua titik yang memiliki fase 1,5 adalah titik P dan V

Jawaban A

iklan header

Pembahasan Soal Gelombang Mekanik dan Stasioner

0 Response to "Pembahasan Soal Gelombang Mekanik dan Stasioner"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel