Pembahasan Soal UTUL UGM 2018 Fisika
Pada kesempatan kali ini, mari kita bedah soal UTUL UGM Fisika tahun 2018 paket 276 untuk mempersiapkan ujian UTUL UGM tahun selanjutnya. Ada beberapa materi yang perlu dipelajari, berikut materi fisika yang dikeluarkan di UTUL UGM Fisika tahun 2018:
1. Usaha dan Energi
2. Kinematika Gerak $($Parabola$)$
3. Fluida Statis
4. Pegas
5. Gaya Lorentz
6. Induksi Elektromagnetik
7. Gaya Lorentz $($ muatan bergerak di samping kawat$)$
8. GHS
9. Bunyi
10. Optik Fisis $($ Celah Tunggal$)$
11. Optik $($Cermin$)$
12. Optik $($Lensa$)$
13. Termodinamika
14. Suhu & Kalor
15. Teori Atom
16. Relativitas
17. Fisika Modern $($ De Broglie$)$
18. Fisika Modern $($ Radiasi Benda Hitam$)$
19. Relativitas Khusus
20. Gravitasi Newton
Berikut soal UTUL UGM Fisika tahun 2018 paket 276
1. Soal
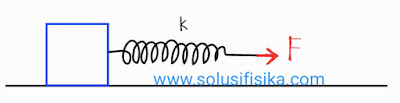
Sebuah balok bermassa $m$ mula - mula bergerak ke kanan pada suatu permukaan horizontal licin dengan kecepatan $v$. Balok tersebut kemudian menekan pegas dengan konstanta pegas $k$. Ketika energi kinetik balok sama dengan energi potensial pegas, besarnya jarak yang ditempuh balok saat menekan pegas adalah?
A. $\displaystyle v\sqrt {\frac {m}{2k}}$
B. $\displaystyle v\sqrt {\frac {m}{k}}$
C. $\displaystyle v\sqrt {\frac {2m}{k}}$
D. $\displaystyle 2v\sqrt {\frac {m}{k}}$
E. $\displaystyle \frac {1}{2}v\sqrt {\frac {m}{k}}$
Pembahasan
Diketahui:
m, v dan pegas k tertekan sejauh x
maka nilai x
\begin{aligned} Ek_{benda}&=\;E_{pegas}\\ \frac{1}{2}mv^{2}&=\frac{1}{2}kx^{2}\\ x^{2}&=\frac{m}{k} v^{2}\\ x&=v\sqrt{\frac{m}{k}} \end{aligned}
Jawaban B
2. Soal
Sebuah peluru bermassa 2 kg yang ditembakkan dari tanah dengan sudut elevasi dan kecepatan awal tertentu memiliki ketinggian maksimum dan jangkauan maksimum berturut -turut 25 m dan 40 m. Energi kinetik peluru pada saat ditembakkan adalah?
A. 500 J
B. 580 J
C. 625 J
D. 800 J
E. 1000 J
Pembahasan
Diketahui:
$m =\;2 \;kg$
$H_{max}=\;25\;m$
$X_{max}=\;40\;m$
maka energi kinetik benda $E_{k}$
\begin{aligned} \frac{H_{max}}{X_{max}}&=\frac{tan\;\alpha}{4}\\ \frac {25}{40}&=\frac{tan\;\alpha}{4}\\ tan\;\alpha&=\frac{5}{2} \end{aligned}
diperoleh $tan\;\alpha =\frac{5}{2}$ maka $sin\;\alpha=\frac{5}{\sqrt{29}}$
dari $H_{max}$ bisa mencari $v_{0}$
\begin{aligned} H_{max}&=\frac{v_{0}^{2}sin^{2}\alpha}{2g}\\ 25&=\frac{v_{0}^{2}(\frac{5}{\sqrt{29}})}{2.10}\\ v_{0}^{2}&=580 \end{aligned}
Nilai energi kinetik benda
\begin{aligned} E_{k}&=\frac{1}{2}mv_{0}^{2}\\ E_{k}&=\frac{1}{2}(2)(580)\\ E_{k}&=\;580\; joule \end{aligned}
Jawaban B
3. Soal
Tekanan total di dalam suatu fluida pada kedalaman $h_{1}$ adalah $P_{1}$. Sedangkan pada kedalaman $h_{2}$, tekanan totallnya adalah $P_{2}$. Jika tekanan atmosfer $P_{0}$ maka tekanan total pada kedalaman $h_{1}+h_{2}$ adalah?
A. $P_{1}+P_{2}$
B. $P_{1}+P_{2}-P_{0}$
C. $P_{1}+P_{2}+P_{0}$
D. $P_{1}+P_{2}-2P_{0}$
E. $P_{1}+P_{2}+2P_{0}$
Pembahasan
Diketahui tekanan total
$P_{1}=P_{0}+\rho.g.h_{1}$
diperoleh $\rho.g.h_{1}=P_{1}-P_{0}$
$P_{2}=P_{0}+\rho.g.h_{2}$
diperoleh $\rho.g.h_{2}=P_{2}-P_{0}$
maka tekanan total di kedalaman $h_{1}+h_{2}$ adalah
\begin{aligned} P_{h_{1}+h_{2}}&=P_{0}+\rho.g.(h_{1}+h_{2})\\ P_{h_{1}+h_{2}}&=P_{0}+\rho.g.h_{1}+\rho.g.h_{2}\\ P_{h_{1}+h_{2}}&=P_{0}+P_{1}-P_{0}+P_{2}-P_{0}\\ P_{h_{1}+h_{2}}&=P_{1}+P_{2}-P_{0} \end{aligned}
Jawaban B
4. Soal
Sebuah pegas ringan memiliki tetapan pegas 500 N/m. Salah satu ujung pegas itu diikat pada balok yang terletak di lantai yang cukup licin, sedangkan ujung yang lain ditarik $($lihat gambar$)$ dengan gaya yang tetap, sehingga balok mengalami percepatan $5\; m/s^{2}$ dan pegas bertambah panjang 1 cm. Jika di atas balok itu diletakkan sebuah balok lain yang bermassa sama sehingga perceptannya menjadi $2,5\; m/s^{2}$, berapakah pertambahan panjang pegas sekarang?
A. 1,0 cm
B. 2,0 cm
C. 2,4 cm
D. 2,8 cm
E. 3,2 cm
Pembahasan
Diketahui
pegas $k =\;500\;N/m$
$a_{1}=5\; m/s^{2}$ dan $x_{1}=1\;cm$
$m_{1}=m$
$a_{1}=5\; m/s^{2}$ dan $x_{2}=. . . . ?$
$m_{2}=2m$
Benda terhubung pegas ditarik dengan gaya F
Rumus
\begin{aligned} F&=kx\\ ma&=kx \end{aligned}
\begin{aligned} \frac{m_{1}.a_{1}}{m_{2}.a_{2}}&=\frac{k.x_{1}}{k.x_{2}}\\ \frac{m_{1}.a_{1}}{m_{2}.a_{2}}&=\frac{x_{1}}{x_{2}}\\ \frac{m.5}{2m. 2,5}&=\frac{x}{x_{2}}\\ x_{2}&=\;1\; cm \end{aligned}
Jawaban A
5. Soal
Sebuah elektron bergerak ke kanan horizontal memasuki suatu wilayah dengan medan magnet seragam mengarah ke atas. Gaya yang dialami elektron saat memasuki wilayah tersebut adalah mengarah?
A. Ke atas
B. Ke bawah
C. Ke luar bidang gambar
D. Masuk bidang gambar
E. Ke kiri
Pembahasan
Muatan Q bergerak kekanan dan medan magnet ke atas
maka gaya lorentz ke arah?
Inget kaidah tangan kanan 2
v = ibu jari
B = banyak jari
F = Q (+) tegak lurus telapak tangan dan Q (-) tegak lurus punggung tangan
6. Soal
Sebuah induktor dengan induktansi 10 mH, sebuah resistor dan baterai ideal dipasangkan dalam rangkaian secara serial. Ketika arus dalam rangkaian adalah 1 A, maka besar energi yang tersimpan dalam induktor adalah?
A. 5 mJ
B. 15 mJ
C. 20 mJ
D. 25 mJ
E. 50 mJ
Pembahasan
Diketahui
$L\;=\;10\;mH=\;10\times 10^{-3}H$
$I\;=\;1\; A$
maka:
\begin{aligned} W&=\frac{1}{2}LI^{2}\\ W&=\frac{1}{2}(10\times 10^{-3})(1^{2}) \\ W&=5\times 10^{-3}J\\ W&= 5\;mJ \end{aligned}
Jawaban A
7. Soal
Sebuah kawat tak hingga panjang beraturan arus listrik $I_{0}$. Sebuah elektron dilepaskan pada jarak $a$ dan kawat dengan kecepatan awal $v_{0}$ menjauhi kawat. Setelah beberapa saat arah gerak elektron menuju kawat, kecepatan elektron ketika itu adalah?
A. $v_{0}$
B. $2v_{0}$
C. $v_{0}\;ln\;3$
D. $\frac {v_{0}}{2}$
E. $v_{0}\;ln\;2$
Pembahasan
Diketahui
Muatan listrik bergerak di samping kawat berarus listrik akan bergerak melingkar beraturan dengan kecepatan konstan $v_{0}$
Jawaban A
8. Soal
Sebuah pegas dengan konstanta pegas $k$ dipakai untuk menggantungkan suatu benda bermassa m. Sistem benda pegas ini kemudian diosilasikan, dan berosilasi dengan periode T. Pegas kemudian dipotong menjadi tiga dan ketiganya dipasangkan ke benda lain secara paralel. Ketika benda kedua diosilasikan, periode osilasinya juga T. Maka massa benda kedua adalah?
A. 3m
B. 6m
C. 9m
D. 12m
E. 15m
Pembahasan
Diketahui
Keadaan awal(A)
$k_{A}=k$ dengan panjang $L$
$m_{A}=m$
$T_{A}=T$
Keadaan akhir (B)
Pegas dipotong menjadi 3 bagian masing - masing $\frac{1}{3}L$
berdasarkan rumus $k=\frac{EA}{L}$ dan $k$ berbanding terbalik dengan L
maka nilai $k$ masing - masing pegas menjadi $k{1}=k{2}=k{3}=3k$
kemudian disusun paralel diperoleh
$k_{B}=3k+3k+3k=9k$
$T_{A}=T$
$m_{B}=?$
berdasarkan rumus $T=2\pi \sqrt{\frac{m}{k}}$
\begin{aligned} T_{A}&={T_{B}}\\ 2\pi \sqrt{\frac{m_{A}}{k_{A}}}&=2\pi \sqrt{\frac{m_{B}}{k_{B}}}\\ \sqrt{\frac{m_{A}}{k_{A}}}&=\sqrt{\frac{m_{B}}{k_{B}}}\\ \frac{m_{A}}{k_{A}}&=\frac{m_{B}}{k_{B}}\\ \frac{m}{k}&=\frac{m_{B}}{9k}\\ m_{B}&=9m \end{aligned}
Jawaban C
9. Soal
Gelombang bunyi dengan frekuensi 256 Hz merambat di udara dengan kecepatan 330 m/s. Cepat rambat gelombang bunyi dengan frekuensi 512 Hz di udara adalah?
A. 82,5 m/s
B. 165 m/s
C. 330 m/s
D. 347,5 m/s
E. 660 m/s
Pembahasan
Cepat rambat bunyi di udara akan selalu konstan walau frekuensi diubah, maka kecepatan bunyi di udara tetap 330 m/s.
Jawaban C
10. Soal
Pada suatu pola difraksi celah tunggal dengan lebar celah a, terdapat difraksi minimum pertama pada sudut $x^{\circ}$. Bila celah tunggal tadi diganti dengan celah ganda berjarak $d$ maka posisi gelap pertama tidak akan berubah bila?
A. $d\;=\;a$
B. $d\;=\frac {a}{2}$
C. $d\;=\frac {a}{\sqrt {2}}$
D. $d\;=\frac {a}{3}$
E. $d\;=\frac {a}{\sqrt {3}}$
Pembahasan
Difraksi celah tunggal(A)
$d_{A} =a$
difraksi minimum pertama (m=1)
$\theta=x^{\circ}$
Interferensi celah ganda(B)
$d_{B}=d$
interferensi keadaan gelap pertama (m=1)
maka :
\begin{aligned} \frac{d_{A}sin\;x^{\circ}}{d_{B}sin\;x^{\circ}}&=\frac{m\lambda}{(m-\frac{1}{2})\lambda}\\ \frac{d_{A}}{d_{B}}&=\frac{m}{m-\frac{1}{2}}\\ \frac{a}{d}&=\frac{1}{1-\frac{1}{2}}\\ \frac{a}{d}&=\frac{1}{\frac{1}{2}}\\ d&=\frac{a}{2} \end{aligned}
Jawaban B
11. Soal
Sebuah benda yang diletakkan 10 cm dari cermin cekung menghasilkan bayangan nyata berjarak 8 cm dari cermin. Jika benda tersebut dipindahkan ke posisi baru sejauh 40 cm dari cermin, maka posisi bayangan dan sifatnya adalah?
A. 3,7 cm di depan cermin, nyata
B. 4,2 cm di belakang cermin, maya
C. 5,0 cm di depan cermin, nyata
D. 6,4 cm di belakang cermin, maya
E. 7,5 cm di depan cermin, nyata
Pembahasan
Diketahui
Cermin cekung
$s_{1}=10\;cm$
$s'_{1}=8\;cm$
$s_{2}=40\;cm$
$s'_{2}=. . . . ?$
maka
cermin tetap, hanya benda yang digeser sehingga nilai $f_{1}=f_{2}$
\begin{aligned} f_{1}&=f_{2}\\ \frac{s_{1}\times s'_{1}}{s_{1}+s'_{1}}&=\frac{s_{2}\times s'_{2}}{s_{2}+s'_{2}}\\ \frac{10\times 8}{10+8}&=\frac{40\times s'_{2}}{40+s'_{2}}\\ \frac{80}{18}&=\frac{40\times s'_{2}}{40+s'_{2}}\\ \frac{1}{9}&=\frac{s'_{2}}{40+s'_{2}}\\ 40+s'_{2}&=9s'_{2}\\ 8s'_{2}&=40\\ s'_{2}&=+5\;cm \end{aligned}
$s'_{2}= +$(positif) berarti bayangan nyata dan di depan cermin
Jawaban C
12. Soal
Dua lenda cembung masing - masing dengan fokus sebesar 15 cm diletakkan terpisah sejauh 40 cm. Jika suatu benda diletakkan 30 cm dari lensa pertama, maka bayangan terakhir yang terbentuk akan memiliki perbesaran total sebesar?
A. 2 kali
B. 3 kali
C. 4 kali
D. 5 kali
E. 6 kali
Pembahasan
Diketahui
Jawaban B
13. Soal
Suatu gas ideal mengalami proses ekspansi. Selama ekspansi energi dalamnya tidak berubah. Bila awalnya tekanannya adalah $1\; \times \;10^{5}Pa$ dan volumenya $1\;m^{3}$, maka berikut ini adalah nilai tekanan dan volumenya yang mungkin bagi gas ideal tadi ?
A. $P=\;1\; \times \; 10^{5}Pa,\;V\;=\;2\;m^{3}$
B. $P=\;2\; \times \; 10^{5}Pa,\;V\;=\;1\;m^{3}$
C. $P=\;2\; \times \; 10^{5}Pa,\;V\;=\;3\;m^{3}$
D. $P=\;0,5\; \times \; 10^{5}Pa,\;V\;=\;2\;m^{3}$
E. $P=\;0,1\; \times \; 10^{5}Pa,\;V\;=\;3\;m^{3}$
Pembahasan
Diketahui
$P_{1}=1\times 10^{5}Pa$ dan $V_{1}=1\;m^{3}$
Energi dalam tidak berubah maka gas mengalami proses isotermal, maka:
\begin{aligned} P_{1}V_{1}&=P_{2}V_{2}\\ 1\times 10^{5}\times 1&=P_{2}V_{2}\\ P_{2}V_{2}&=1\times 10^{5} \end{aligned}
Maka nilai tekanan dan volume yang mungkin adalah $P_{2}=\;0,5\; \times \; 10^{5}Pa,\;V_{2}\;=\;2\;m^{3}$
Jawaban D
14. Soal
Pada saat air membeku termometer $X$ menunjukkan angka $-10^{\circ}X$ dan pada saat mendidih menunjukkan angka $140^{\circ}X$. Jika termometer Celcius menunjukkan angka $30^{\circ}C$, maka termometer $X$ akan menunjukkan angka?
A. $30^{\circ}X$
B. $35^{\circ}X$
C. $37,5^{\circ}X$
D. $40^{\circ}X$
E. $45^{\circ}X$
Pembahasan
Diketahui
Termometer X
titik beku $-10^{\circ}X$ dan titik didih $140^{\circ}X$
maka $30^{\circ}C= . . . . ^{\circ}X$
\begin{aligned} \frac{T-(-10)}{140-(-10)}&=\frac{30-0}{100-0}\\ \frac{T+10}{150}&=\frac{30}{100}\\ \frac{T+10}{15}&=\frac{3}{1}\\ T+10&=45\\ T&=\;35^{\circ}X \end{aligned}
Jawaban B
15. Soal
Pada atom Hidrogen, besar jari - jari kulit elektron nomor $n$ dan momentum sudutnya berturut - turut adalah $r_{n}$ dan $L_{n}$ dengan konstanta positif $C$ adalah?
A. $\frac {L^{2}_{n}}{r_{n}}=C$
B. $\frac {L_{n}}{r_{n}}=C$
C. $L_{n}r_{n}=C$
D. $\frac {r^{2}_{n}}{L_{n}}=C$
E. $L^{2}_{n}r_{n}=C$
Pembahasan
Momentum sudut menurut teori atom Bohr
$L_{n}=n\frac{h}{2\pi}$
Jari - jari orbit elektron di kulit ke - n
$r_{n}=n^{2}r_{0}$ maka $n=\sqrt{\frac{r_{n}}{r_{0}}}$
maka
\begin{aligned} L_{n}&=n\frac{h}{2\pi}\\ L_{n}&=\sqrt{\frac{r_{n}}{r_{0}}}\left(\frac{h}{2\pi}\right)\\ \frac{L^{2}_{n}}{r_{n}}&=\frac{h^{2}}{4\pi^{2}r_{0}}\\ \frac{L^{2}_{n}}{r_{n}}&=C \end{aligned}
Jawaban A
16. Soal
Suatu partikel bergerak dengan kecepatan 0,4 c sepanjang sumbu x pada kerangka S'. Jika kerangka S' bergerak dengan kecepatan 0,6 c terhadap kerangka S searah dengan arah kecepatan partikel, maka kecepatan partikel relatif terhadap S adalah sebesar?
A. 0,2c
B. 0,4c
C. 0,6c
D. 0,8c
E. 1,0c
Pembahasan
Diketahui
A = partikel
B = kerangka S'
C = kerangka S
$v_{AB}=\;0,4c$
$v_{BC}=\;0,6c$
$v_{AC}= . . . . ?$
\begin{aligned} v_{AC}&=\frac{v_{AB}+v_{BC}}{1+\frac{v_{AB}.v_{BC}}{c^{2}}}\\ v_{AC}&=\frac{0,4c+0,6c}{1+\frac{0,4c.0,6c}{c^{2}}}\\ v_{AC}&=\frac{1c}{1,24}\\ v_{AC}&=\;0,8c \end{aligned}
Jawaban D
17. Soal
Sebuah partikel bermassa $m$ dan bermuatan $+q$ dipercepat dari keadaan diam menuju beda potensial $V$, kemudian memasuki medan magnet seragam $B$ yang arahnya tegak lurus kecepatan partikel. Jari - jari lintasan partikel adalah?
A. $\displaystyle \sqrt {\frac {2mV}{qB}}$
B. $\displaystyle \sqrt {\frac {mV}{qB^{2}}}$
C. $\displaystyle \sqrt {\frac {mV}{qB}}$
D. $\displaystyle \sqrt {\frac {mV}{qB^{2}}}$
E. $\displaystyle \sqrt {\frac {2mV}{qB^{2}}}$
Pembahasan
Diketahui
partikel bermassa $m$, bermuatan $q$ dipercepat dengan potensial listrik $V$ dan memasuki medan magnet $B$ membentuk lintasan lingkaran.
Energi kinetik = Energi Potensial
\begin{aligned} E_{k}&=E_{p}\\ \frac{1}{2}mv^{2}&=qV\\ v&=\sqrt{\frac{2qV}{m}} \end{aligned}
Jari - jari lintasan (R)
\begin{aligned} R&=\frac{mv}{Bq}\\ R&=\frac{m}{Bq}\sqrt{\frac{2qV}{m}}\\ R&=\sqrt{\frac{2mV}{qB^{2}}} \end{aligned}
Jawaban E
18. Soal
Suatu benda hitam pada suhu $T\;(K)$ memancarkan energi $E$. Jika dinaikkan suhunya sebesar $200^{\circ}C$, energinya adalah $16E$. Jika kemudian dinaikkan lagi sebesar $200^{\circ}C$, energinya adalah $nE$. Nilai $n$ adalah?
A. 32
B. 81
C. 256
D. 324
E. 1024
Pembahasan
Diketahui
Radiasi Benda Hitam
$T_{1}=\;T$
$Q_{1}=\;E$
$T_{2}=\;T+200$
$Q_{2}=\;16E$
$T_{3}=\;T+200+200=\;T+400$
$Q_{2}=\;nE$
Berdasarkan rumus $\frac{Q}{t}=e\sigma A T^{4}$ maka $Q$ sebanding $T^{4}$
\begin{aligned} \frac{Q_{1}}{Q_{2}}&=\frac{T^{4}_{1}}{T^{4}_{2}}\\ \frac{E}{16E}&=\frac{T^{4}}{(T+200)^{4}}\\ \frac{1}{2}&=\frac{T}{T+200}\\ T+200&=\;2T\\ T&=\;200\; K \end{aligned}
maka
\begin{aligned} \frac{Q_{1}}{Q_{3}}&=\frac{T^{4}_{1}}{T^{4}_{3}}\\ \frac{E}{nE}&=\frac{200^{4}}{(400+200)^{4}}\\ \frac{1}{n}&=\left(\frac{200}{600}\right)^{4}\\ \frac{1}{n}&=\frac{1}{81}\\ n&=\;81\; \end{aligned}
Jawaban B
19. Soal
Suatu partikel relativistik memikiki energi diam $E_{0}$, momentum $p$ dan energi kinetik $K$. Misalnya $\frac {pc}{E_{0}}=x$, maka $\frac {K}{E_{0}}= . . . . $
A. $-1 + \sqrt {1+x^{2}}$
B. $-1 + \sqrt {1-x^{2}}$
C. $1 - \sqrt {x^{2}-1}$
D. $1- \sqrt {1-x^{2}}$
E. $1 + \sqrt {1-x^{2}}$
Pembahasan
Diketahui
Energi diam $E_{0}$, Momentum linear $p$ dan Energi Kinetik $K$
$\frac {pc}{E_{0}}=x$
$\frac {K}{E_{0}}= . . . . ?$
Energi Total (E)
\begin{aligned} E&=E_{0}+E_{k}\\ E_{k}&=E-E_{0}\\ K&=E-E_{0}\end{aligned}
dan \begin{aligned} E^{2}&=E^{2}_{0}+p^{2}c^{2}\\ E&=\sqrt{E^{2}_{0}+p^{2}c^{2}} \end{aligned}
\begin{aligned} \frac{K}{E_{0}}&=\frac{E-E_{0}}{E_{0}}\\ \frac{K}{E_{0}}&=\frac{E}{E_{0}}-1\\ \frac{K}{E_{0}}&=\frac{\sqrt{E^{2}_{0}+p^{2}c^{2}}}{E_{0}}-1\\ \frac{K}{E_{0}}&=-1+\sqrt{\frac{E^{2}_{0}+p^{2}c^{2}}{E^{2}_{0}}}\\ \frac{K}{E_{0}}&=-1+\sqrt{1+\left(\frac{pc}{E_{0}}\right)^{2}}\\ \frac{K}{E_{0}}&=-1+\sqrt{1+x^{2}} \end{aligned}
Jawaban A
20. Soal
Bila diketahui jarak bumi dan bulan adalah 380.000 km dan jari - jari bumi adalah 6400 km, maka kecepatan minimum yang dibutuhkan bulan untuk lepas dari pengaruh gravitasi bumi adalah?. . . . m/s
A. 1453
B. 145,3
C. 14,53
D. 1,453
E. 0,1453
Pembahasan
$R=\;6400\;km=\;6.400.000\;m$
$r=380.000\;km=\;380.000.000\;m$
Kecepatan lepas $(v_{lepas})$?
\begin{aligned} v_{lepas}&=R\sqrt{\frac{2g}{r}}\\ v_{lepas}&=6400000\sqrt{\frac{2.(9,8)}{380000000}}\\ v_{lepas}&=1453,5\;m/s \end{aligned}
Jawaban A
Untuk mendapatkan pembahasan soal di atas, silakan klik " download "
Pembahasan Soal UTUL UGM 2018 dapat dilihat pada channel youtube di bawah ini.